Question

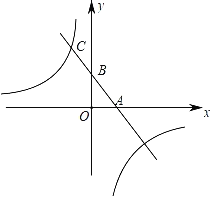
【题目】如图，在平面直角坐标系中，已知△ABC，∠ABC=90°，顶点A在第一象限，B、C在x轴的正半轴上（C在B的右侧），BC=3，AB=4，若双曲线交边AB于点E，交边AC于中点D．

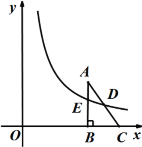
（1）若OB=2，求k；

（2）若AE=， 求直线AC的解析式．

Answer 1

【答案】（1）7；（2）y=-x+12.

【解析】

（1）过D作BC垂线，根据D为中点，得到D点坐标，代入可求得结果；

（2）设OB为a，E，D点坐标为关于a的代数式，代入函数可求得a值，继而可得到A，C点坐标，根据已知直线上两点，求直线解析式，即可求得AC解析式．

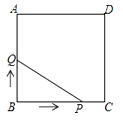
（1）如图，

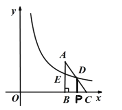
过D作BC垂线，交BC于P点，

∵BC=3，D为AC中点，

∴BP=BC=，

∵OB=2，∴OP=，∴P点坐标为（，0）

∵AB=4，∴D点坐标为（，2），

∵D在y=上，代入D点坐标，

∴k=7；

故答案为7；

（2）∵AE=AB=×4=，

∴BE=AB-AE=4-=，

设OB=a，则E点坐标为（a，），D点坐标为（a+，2），

∵D，E在y=上，

∴k=xy=a=2(a+)，

∴a=6，

∴A点坐标为（6,4），C点坐标为（9,0），

设AC的解析式为y=kx+b，A，C坐标代入，

求得k=-，b=12，

故AC的解析式为y=-x+12．