题目内容
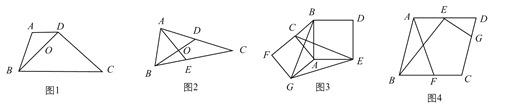
【题目】如图1,我们把对角线互相垂直的四边形叫做对垂四边形.
观察发现:如图1,对垂四边形ABCD四边存在数量为: AD2+BC2=AB2+CD2.
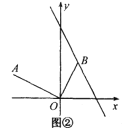
应用发现:如图2,若AE,BD是△ABC的中线,AE⊥BD,垂足为O,AC=4,BC=6,求AB=
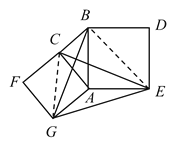
应用知识:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=![]() ,AB=
,AB=![]() 求GE长.
求GE长.
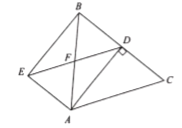
拓展应用:如图4,在平行四边形ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=4,AB=3,求AF的长
【答案】应用发现:![]() ;应用知识:3;拓展应用:
;应用知识:3;拓展应用:![]()
【解析】
应用发现:连接DE,构成对垂四边形,再根据对垂四边形ABCD四边存在数量关系进行计算即可;
应用知识:先证明CE⊥BG得到四边形CGEB是对垂四边形,再根据结论进行计算即可;
拓展应用:连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,连接PH,先证明四边形APHE是对垂四边形和EP、AH是△AFE的中线,再根据对垂四边形的性质求得AP的长度,从而求得AF的长度.
应用发现:
连接DE,如图所示:
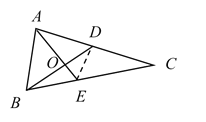
∵AE,BD是△ABC的中线,AC=4,BC=6,
∴AD=2,BE=3,DE=![]() ,
,
∵AE⊥BD,垂足为O,
∴四边形ABED是对垂四边形,
∴AB2+DE2=AD2+BE2,
∴AB2+![]() =22+32,
=22+32,
∴AB=![]() ;
;
应用知识:
连接CG、BE,如图所示:
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
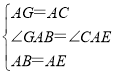 ,
,
∴△GAB≌△CAE,
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是对垂四边形,
∴CG2+BE2=CB2+GE2,
∵AC=![]() ,AB=
,AB=![]() ,
,
∴BC=1,CG=![]() ,BE=
,BE=![]() ,
,
∴22+![]() =12+GE2,
=12+GE2,
∴GE=3;
拓展应用:
(3)如图,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,连接PH,

∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∴四边形APHE是对垂四边形,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=4,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴AE=![]() AD,BF=
AD,BF=![]() BC,
BC,
∴AE=BF![]() AD=2,
AD=2,
又∵AE∥BF,
∴四边形ABFE是平行四边形,
∴EF=AB=3,AP=PF,
∴EP分别是△AFE的中线,
在△AEH和△CFH中,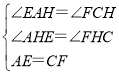 ,
,
∴△AEH≌△CFH(AAS),
∴EH=FH,
∴AH分别是△AFE的中线,
∴PH=![]() ,EH=
,EH=![]() ,
,
∵四边形APHE是对垂四边形,
∴PH2+AE2=EH2+AP2,
∴12+22=![]() +AP2,
+AP2,
∴AP=![]() ,
,
又∵EP分别是△AFE的中线,
∴AF=2AP=![]() .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案