题目内容
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).
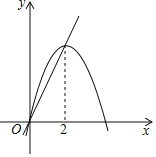
【答案】②③
【解析】①观察函数图象,可知:当x>2时,抛物线y1=-x2+4x在直线y2=2x的下方,进而可得出当x>2时,M=y1,结论①错误;
②观察函数图象,可知:当x<0时,抛物线y1=-x2+4x在直线y2=2x的下方,进而可得出当x<0时,M=y1,再利用二次函数的性质可得出M随x的增大而增大,结论②正确;
③利用配方法可找出抛物线y1=-x2+4x的最大值,由此可得出:使得M大于4的x的值不存在,结论③正确;
④利用一次函数图象上点的坐标特征及二次函数图象上点的坐标特征求出当M=2时的x值,由此可得出:若M=2,则x=1或2+![]() ,结论④错误.
,结论④错误.
此题得解.
①当x>2时,抛物线y1=-x2+4x在直线y2=2x的下方,
∴当x>2时,M=y1,结论①错误;
②当x<0时,抛物线y1=-x2+4x在直线y2=2x的下方,
∴当x<0时,M=y1,
∴M随x的增大而增大,结论②正确;
③∵y1=-x2+4x=-(x-2)2+4,
∴M的最大值为4,
∴使得M大于4的x的值不存在,结论③正确;
④当M=y1=2时,有-x2+4x=2,
解得:x1=2-![]() (舍去),x2=2+
(舍去),x2=2+![]() ;
;
当M=y2=2时,有2x=2,
解得:x=1.
∴若M=2,则x=1或2+![]() ,结论④错误.
,结论④错误.
综上所述:正确的结论有②③.
故答案为:②③.

练习册系列答案
相关题目