题目内容
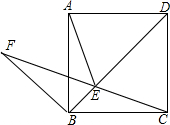 如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE.延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
如图,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连接AE,CE.延长CE到F,连接BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
| ||
| 2 |
③BE+EC=EF;④S△AED=
| 1 |
| 4 |
| ||
| 8 |
| ||
| 12 |
其中正确的个数是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
分析:根据正方形的性质推出AB=BC,∠ABD=∠CBD=45,证△ABE≌△CBE,即可判断①;过F作FH⊥BC于H,根据直角三角形的性质即可求出FH;过A作AM⊥BD交于M,根据勾股定理求出BD,根据三角形的面积公式即可求出高AM,根据三角形的面积公式求出即可.
解答: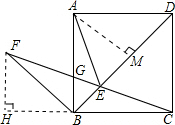 解:∵正方形ABCD,
解:∵正方形ABCD,
∴AB=BC,∠ABD=∠CBD=45°,
∵BE=BE,
∴△ABE≌△CBE,
∴AE=CE,∴①正确;
∵过F作FH⊥BC于H,
∵BF=BC=1,
∴∠BFC=∠FCB=15°,
∴FH=
BF=
,∴②错误;
∵Rt△BHF中,
FH=
,BF=1,
∴CF=
=2+
∵BD是正方形ABCD的对角线,
∴AE=CE,
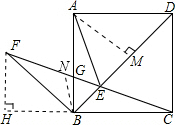
在EF上取一点N,使BN=BE,
又∵∠NBE=∠EBC+∠ECB=45°+15°=60°,
∴△NBE为等边三角形,
∴∠ENB=60°,
又∵∠NFB=15°,
∴∠NBF=45°,
又∵∠EBC=45°,
∴∠NBF=∠EBC,
又∵BF=BC,∠NFB=∠ECB=15°,
可证△FBN≌△CBE,
∴NF=EC,
故BE+EC=EN+NF=EF,
∴③正确;
过A作AM⊥BD交于M,
根据勾股定理求出BD=
,
由面积公式得:
AD×AB=
BD×AM,
AM=
=
,
∵∠ADB=45°,∠AED=60°,
∴DM=
,EM=
,
∴S△AED=
DE×AM=
+
,∴④错误;
S△EBF=S△FBC-S△EBC=
×1×
-
×1×[1-
]=
,∴⑤正确.
故选B.
 解:∵正方形ABCD,
解:∵正方形ABCD,∴AB=BC,∠ABD=∠CBD=45°,
∵BE=BE,
∴△ABE≌△CBE,
∴AE=CE,∴①正确;
∵过F作FH⊥BC于H,
∵BF=BC=1,
∴∠BFC=∠FCB=15°,
∴FH=
| 1 |
| 2 |
| 1 |
| 2 |
∵Rt△BHF中,
FH=
| 1 |
| 2 |
∴CF=
(
|
| 3 |
∵BD是正方形ABCD的对角线,
∴AE=CE,

在EF上取一点N,使BN=BE,
又∵∠NBE=∠EBC+∠ECB=45°+15°=60°,
∴△NBE为等边三角形,
∴∠ENB=60°,
又∵∠NFB=15°,
∴∠NBF=45°,
又∵∠EBC=45°,
∴∠NBF=∠EBC,
又∵BF=BC,∠NFB=∠ECB=15°,
可证△FBN≌△CBE,
∴NF=EC,
故BE+EC=EN+NF=EF,
∴③正确;
过A作AM⊥BD交于M,
根据勾股定理求出BD=
| 2 |
由面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
AM=
| 1 | ||
|
| ||
| 2 |
∵∠ADB=45°,∠AED=60°,
∴DM=
| ||
| 2 |
| ||
| 6 |
∴S△AED=
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 12 |
S△EBF=S△FBC-S△EBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(
| ||||||
| 1 |
| ||
| 12 |
故选B.
点评:本题主要考查对正方形的性质,全等三角形的性质和判定,三角形的面积,勾股定理,含30度角的直角三角形的性质等知识点的理解和掌握,综合运用这些性质进行证明是解此题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6