题目内容
【题目】如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。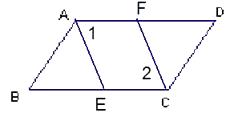
试说明:
(1)AE∥CF;
(2)AB∥CD。
【答案】
(1)解:∵AD∥CB (已知)
∴ ∠1=∠AEB (两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴ ∠AEB= ∠2(等量代换)
∴AE∥CF(同位角相等,两直线平行)
(2)解:∵三角形ABE的内角和是180 ∴∠B+∠BAE+∠AEB=180
又∵∠AEB= ∠2(已证) ∠BAE=∠DCF(已知)
∴∠B+∠2+∠DCF=180 即∠B+∠BCD=180
∴AB∥CD(同旁内角互补,两直线平行)
【解析】(1)根据平行线的性质两直线平行,内错角相等得出∠1=∠AEB ,根据等量代换得出∠AEB= ∠2 ,根据平行线的判断同位角相等,两直线平行得出AE∥CF ;
(2)根据三角形的内角和得出∠B+∠BAE+∠AEB=180 ,又∠AEB= ∠2 , ∠BAE=∠DCF ,利用等量代换得出∠B+∠2+∠DCF=180 , 即∠B+∠BCD=180 ,根据平行线的判断同旁内角互补,两直线平行得出AB∥CD 。

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目