题目内容
 已知抛物线y=
已知抛物线y=| 1 |
| 2 |
(1)确定此抛物线的对称轴方程和顶点坐标;
(2)如图,若直线l:y=kx(k>0)分别与抛物线交于两个不同的点A、B,与直线y=-x+4相交于点P,试证
| OP |
| OA |
| OP |
| OB |
(3)在(2)中,是否存在k值,使A、B两点的纵坐标之和等于4?如果存在,求出k值;如果不存在,请说明理由.
分析:(1)将抛物线的解析式化为顶点式,即可得出抛物线的对称轴方程和顶点坐标.
(2)可通过构建相似三角形将
和
进行适当转换,分别过A、P、B作x轴的垂线,设垂足为A′、P′、B′;那么
和
就可转换成P、A的横坐标比以及P、B的横坐标比.由于A、B、P均为函数的交点,因此可联立相关函数,根据韦达定理进行求解.
(3)可根据直线y=kx的解析式,用A、B的横坐标表示出各自的纵坐标,然后根据韦达定理和两点的纵坐标和为4求出k的值,由于两函数有两个不同的交点,因此两函数联立的方程△>0,可得出一个k的取值范围,然后根据这个范围判定k的值是否符合要求即可.
(2)可通过构建相似三角形将
| OP |
| OA |
| OP |
| OB |
| OP |
| OA |
| OP |
| OB |
(3)可根据直线y=kx的解析式,用A、B的横坐标表示出各自的纵坐标,然后根据韦达定理和两点的纵坐标和为4求出k的值,由于两函数有两个不同的交点,因此两函数联立的方程△>0,可得出一个k的取值范围,然后根据这个范围判定k的值是否符合要求即可.
解答:(1)解:抛物线y=
x2-x+2=
(x-1)2+
,
所以抛物线的对称轴为x=1,顶点坐标为(1,
)
(2)证明:由
,
得x2-2(k+1)x+4=0.
设A(x1,y1)、B(x2,y2),则
x1+x2=2(k+1),x1x2=4;
由
,
得x=
(k>0).
即P点的横坐标xP=
;
作AA′⊥x轴于A′,PP′⊥x轴于P′,BB′⊥x轴于B′,于是:
+
=
+
=
+
=
=
•
=2.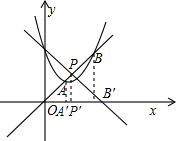
(3)解:不存在.
因为A(x1,y1)、B(x2、y2)在直线y=kx上,由题意,得
y1+y2=kx1+kx2=k(x1+x2)=k•2(k+1)=4;
所以k2+k-2=0.
解得k=1,k=-2(舍去)
当k=1时,方程x2-2(k+1)x+4=0可化为x2-4x+4=0有两个相等的实数根,不同题意舍去
故适合条件的k值不存在.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以抛物线的对称轴为x=1,顶点坐标为(1,
| 3 |
| 2 |
(2)证明:由
|
得x2-2(k+1)x+4=0.
设A(x1,y1)、B(x2,y2),则
x1+x2=2(k+1),x1x2=4;
由
|
得x=
| 4 |
| k+1 |
即P点的横坐标xP=
| 4 |
| k+1 |
作AA′⊥x轴于A′,PP′⊥x轴于P′,BB′⊥x轴于B′,于是:
| OP |
| OA |
| OP |
| OB |
| OP′ |
| OA′ |
| OP′ |
| OB′ |
| xp |
| x1 |
| xp |
| x2 |
| xp(x1+x2) |
| x1x2 |
| 4 |
| k+1 |
| 2(k+1) |
| 4 |

(3)解:不存在.
因为A(x1,y1)、B(x2、y2)在直线y=kx上,由题意,得
y1+y2=kx1+kx2=k(x1+x2)=k•2(k+1)=4;
所以k2+k-2=0.
解得k=1,k=-2(舍去)
当k=1时,方程x2-2(k+1)x+4=0可化为x2-4x+4=0有两个相等的实数根,不同题意舍去
故适合条件的k值不存在.
点评:本题主要考查了函数与一元二次方程的关系、一元二次方程根与系数的关系、函数图象交点等知识.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
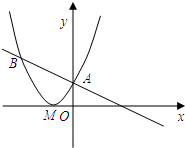 角形?若存在,求出点P的坐标;若不存在,请说明理由.
角形?若存在,求出点P的坐标;若不存在,请说明理由.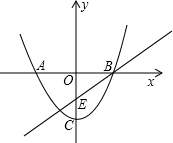 已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=
已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=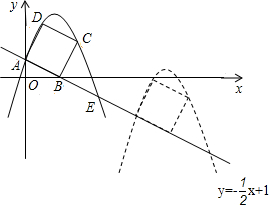
 如图,已知直线
如图,已知直线 +12x-19的顶点的横坐标是3,则a=________.
+12x-19的顶点的横坐标是3,则a=________.