题目内容
如图,已知直线y=-| 1 |
| 2 |
(1)点C的坐标为
(2)若正方形以每秒
| 5 |
(3)在(2)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
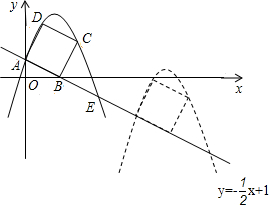
分析:(1)由正方形的性质,可直接求出C,D的坐标,然后可求出抛物线解析式;
(2)动点问题的解决应找到特殊分界点进行讨论,当点A运动到点F时,t=1,当0<t≤1时,当点C运动到x轴t=2,当点D运动到x轴上时,t=3,当2<t≤3时,分别得出函数解析式;
(3)根据阴影部分比较特殊,可以转化为矩形的面积,从而求出.
(2)动点问题的解决应找到特殊分界点进行讨论,当点A运动到点F时,t=1,当0<t≤1时,当点C运动到x轴t=2,当点D运动到x轴上时,t=3,当2<t≤3时,分别得出函数解析式;
(3)根据阴影部分比较特殊,可以转化为矩形的面积,从而求出.
解答: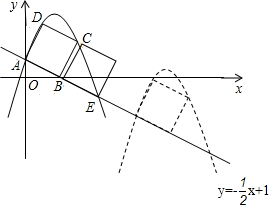 解:(1)∵A在y轴上,B在x轴上,则
解:(1)∵A在y轴上,B在x轴上,则
A(0,1),B(2,0)
C(3,2),D(1,3)
过点A,D,C的抛物线:y=-
x2+
x+1
与直线交点为A(0,1),E(4,-1)
所以点E坐标为(4,-1);
(2)①当点A运动到点B时,t=1,当0<t≤1时,
∵∠OBA=∠GBB′,
tan∠OBA=
=
,
∴tan∠GFB′=
=
=
,
∴GB′=
t,
∴S△BB′G=
BB′×GB′=
×
t×
t=
t2;
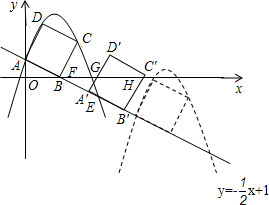
②当点C运动到x轴t=2,
当1<t≤2时,
A′B′=AB=
=
,
∴A′F=
t-
,
∴A′G=
,
∵B′H=
t,
∴S梯形A′B′HG=
(A′G+B′H)×A′B′,
=
(
+
t)×
,
=
t-
;
③当点D运动到x轴上时,t=3,当2<t≤3时,
∵A′G=
,∴GD′=
-
=
,
∵S△AOF=
×1×2=1,OA=1,
∵△AOF∽△GD′H,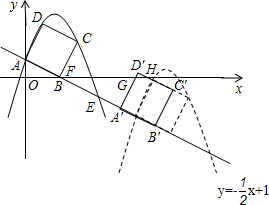
∴
=(
)2,
∴S△GD′H=(
)2,
∴S五边形GA′B′C′H=(
)2-(
)2=-
t2+
t-
;
(3)∵t=3,BB′=AA′=3
,
∴S阴影=S矩形BB′C′C=S矩形AA′D′D=AD×AA′=
×3
=15.
 解:(1)∵A在y轴上,B在x轴上,则
解:(1)∵A在y轴上,B在x轴上,则A(0,1),B(2,0)
C(3,2),D(1,3)
过点A,D,C的抛物线:y=-
| 5 |
| 6 |
| 17 |
| 6 |
与直线交点为A(0,1),E(4,-1)
所以点E坐标为(4,-1);
(2)①当点A运动到点B时,t=1,当0<t≤1时,
∵∠OBA=∠GBB′,
tan∠OBA=
| OA |
| OB |
| 1 |
| 2 |
∴tan∠GFB′=
| GB′ |
| BB′ |
| GB′ | ||
|
| 1 |
| 2 |
∴GB′=
| ||
| 2 |
∴S△BB′G=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
| 5 |
| 4 |
②当点C运动到x轴t=2,
当1<t≤2时,
A′B′=AB=
| 2 2+12 |
| 5 |
∴A′F=
| 5 |
| 5 |
∴A′G=
| ||||
| 2 |

∵B′H=
| ||
| 2 |
∴S梯形A′B′HG=
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||||
| 2 |
| ||
| 2 |
| 5 |
=
| 5 |
| 2 |
| 5 |
| 4 |
③当点D运动到x轴上时,t=3,当2<t≤3时,
∵A′G=
| ||||
| 2 |
| 5 |
| ||||
| 2 |
3
| ||||
| 2 |
∵S△AOF=
| 1 |
| 2 |
∵△AOF∽△GD′H,

∴
| S △GDH |
| S △AOF |
| GD′ |
| OA |
∴S△GD′H=(
3
| ||||
| 2 |
∴S五边形GA′B′C′H=(
| 5 |
3
| ||||
| 2 |
| 5 |
| 4 |
| 15 |
| 2 |
| 25 |
| 4 |
(3)∵t=3,BB′=AA′=3
| 5 |
∴S阴影=S矩形BB′C′C=S矩形AA′D′D=AD×AA′=
| 5 |
| 5 |
点评:此题主要考查二次函数解析式的求法,以及动点问题,动点问题的解决关键是找到特殊分界点,进行讨论是解决问题的关键,此题综合性较强,分析过程中必须细心.

练习册系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )