Question

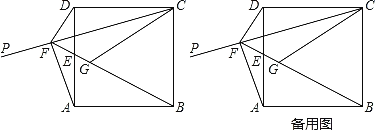
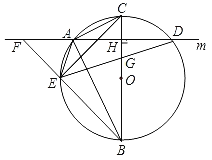
【题目】如图，在⊙O的内接△ABC中，∠CAB＝90°，AB＝2AC，过点A作BC的垂线m交⊙O于另一点D，垂足为H，点E为上异于A，B的一个动点，射线BE交直线m于点F，连接AE，连接DE交BC于点G．

（1）求证：△FED∽△AEB；

（2）若＝，AC＝2，连接CE，求AE的长；

（3）在点E运动过程中，若BG＝CG，求tan∠CBF的值．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）根据同角的余角重叠得出∠EAB＝∠ECB，然后根据三角形相似的判定定理判定即可得出结论；

（2）根据相交弦定理得出DH＝AH＝，再根据勾股定理得，BH＝，进而求出BE＝CE＝，进而求出EF＝，FD＝，借助（1）的结论即可得出结论；

（3）根据平行线分线段成比例得出判，根据平行线的性质得出tan∠CBF＝tan∠CGT＝，根据圆周角定理得出tan∠CED＝tan∠ABC，进而得出，再结合已知条件，即可得出结论．

解：（1）∵⊙O的内接△ABC中，∠CAB＝90°，

∴BC是⊙O的直径，

∵点E为上异于A，B的一个动点，

∴∠CEB＝90°，

∴∠ECB+∠EBC＝90°，

∵过点A作BC的垂线m交⊙O于另一点D，垂足为H，

∴∠FHB＝90°，

∴∠FBH+∠HFB＝90°，

∴∠HFB＝∠ECB，

∵∠EAB＝∠ECB，

∴∠EAB＝∠HFB，

∵∠FBA＝∠ADE，

∴△FED∽△AEB；

（2）∵∠CAB＝90°，AB＝2AC，AC＝2，

∴AB＝4，

根据勾股定理得，BC＝2，

∵AD⊥BC，BC是⊙O的切线，

∴DH＝AH＝＝＝，

在Rt△AHB中，根据勾股定理得，BH＝＝，

∵，BC是⊙O的直径，

∴BE＝CE，∠ECB＝∠EBC＝45°，

∵BC＝2，∠BEC＝90°，

∴BE＝CE＝，

∵∠FHB＝90°，∠EBC＝45°，BH＝，

∴FH＝BH＝，BF＝，

∴EF＝BF﹣BE＝，FD＝FH+DH＝，

∵△FED∽△AEB，

∴，

∴，

∴AE＝；

（3）如图，过点G作GT⊥CE于T，

∵∠CEB＝90°，

∴TG∥EB，

∴，∠CGT＝∠CBF，

∴tan∠CBF＝tan∠CGT＝，

∵，

∴∠CED＝∠ABC，

∴tan∠CED＝tan∠ABC，

∴，

∵，BG＝CG，

∴ET＝CT，，

∴，

∴tan∠CBF＝tan∠CGT＝．