题目内容
△ABC中,AB=AC,∠BAC=90°,D为BC中点,DE⊥DF,若BE=12,CF=5,求EF的长.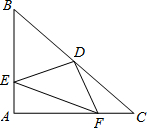

方法一:如图1,延长ED至M,使MD=ED,连接CM,FM,
∵D为BC中点,
∴BD=CD,
在△BDE和△CDM中,
∵
,
∴△BDE≌△CDM(SAS),
∴CM=BE,∠B=∠MCD=45°,
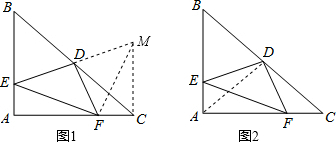
∴∠MCF=∠MCD+∠ACB=45°+45°=90°,
在Rt△MCF中,MF=
=
=13,
∵DE⊥DF,MD=ED,
∴EF=MF=13;
方法二:如图2,连接AD,
∵△ABC是等腰直角三角形,点D为BC的中点,
∴AD=CD,∠DAE=∠C=45°,AD⊥BC,
∴∠ADF+∠CDF=90°,
∵DE⊥DF,
∴∠ADE+∠ADF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∵
,
∴△ADE≌△CDF(ASA),
∴AE=CF,
同理可得AF=BE,
在Rt△AEF中,EF=
=
=13.
∵D为BC中点,
∴BD=CD,
在△BDE和△CDM中,
∵
|
∴△BDE≌△CDM(SAS),
∴CM=BE,∠B=∠MCD=45°,

∴∠MCF=∠MCD+∠ACB=45°+45°=90°,
在Rt△MCF中,MF=
| CM2+CF2 |
| 122+52 |
∵DE⊥DF,MD=ED,
∴EF=MF=13;
方法二:如图2,连接AD,
∵△ABC是等腰直角三角形,点D为BC的中点,
∴AD=CD,∠DAE=∠C=45°,AD⊥BC,
∴∠ADF+∠CDF=90°,
∵DE⊥DF,
∴∠ADE+∠ADF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
∵
|
∴△ADE≌△CDF(ASA),
∴AE=CF,
同理可得AF=BE,
在Rt△AEF中,EF=
| AE2+AF2 |
| 52+122 |

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, 15、如图,在△ABC中,AB=AC,点D,E在直线BC上运动.如果∠DAE=l05°,△ABD∽△ECA,则∠BAC=
15、如图,在△ABC中,AB=AC,点D,E在直线BC上运动.如果∠DAE=l05°,△ABD∽△ECA,则∠BAC= △ABC中,AB=AC,D、E分别是AB、AC的中点,若AB=4,BC=6,则△ADE的周长是
△ABC中,AB=AC,D、E分别是AB、AC的中点,若AB=4,BC=6,则△ADE的周长是 ,连接AO、BE、DC.
,连接AO、BE、DC.