题目内容
【题目】如图，Rt△ABO的顶点A是双曲线y= 
与直线y=﹣x﹣（k+1）在第二象限的交点．AB⊥x轴于B，且S△ABO= 
．
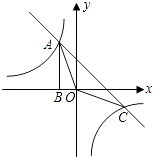
（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积．
【答案】
（1）解：设A点坐标为（x，y），且x＜0，y＞0，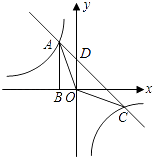 
则S△ABO= 
|BO||BA|= （﹣x）y= 
，
∴xy=﹣3，
又∵y= 
，
即xy=k，
∴k=﹣3．
∴所求的两个函数的解析式分别为y=﹣ 
，y=﹣x+2；
（2）解：由y=﹣x+2，
令x=0，得y=2．
∴直线y=﹣x+2与y轴的交点D的坐标为（0，2），
A、C两点坐标满足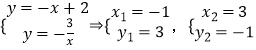 
∴交点A为（﹣1，3），C为（3，﹣1），
∴S△AOC=S△ODA+S△ODC= OD（|x1|+|x2|）= ×2×（3+1）=4．
【解析】两解析式的k一样，根据面积计算双曲线中的k较易，由公式
=2S△ABO,可求出k；（2）求交点就求两解析式联立的方程组的解，可分割△AOC为S△ODA+S△ODC，即可求出.
练习册系列答案
相关题目
【题目】某校举行了“文明在我身边”摄影比赛．已知每幅参赛作品成绩记为x分(60≤x＜100)．校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题：
(1)统计表中c的值为________；样本成绩的中位数落在分数段________中；
(2)补全频数直方图；
(3)若80分以上(含80分)的作品将被组织展评，试估计全校被展评的作品数量是多少．
