题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,CD与CE分别是斜边AB上的高与中线,则下列结论:①BE=BC;②∠DCB=∠A;③∠DCB=∠ACE;④![]() ,其中正确的结论是_____.
,其中正确的结论是_____.
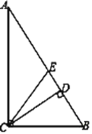
【答案】②③④
【解析】
根据斜边上的中线等于斜边的一半,得BE=CE≠BC,故①错误;根据直角三角形的性质得到AE=CE=BE,根据等腰三角形的性质得到∠A=∠ACE,于是得到∠DCB=∠ACE,故②正确;同理得到∠ACD=∠BCE,故③正确;由于CD⊥AB,且CE=![]() AB,可得
AB,可得![]() =
=![]() AB·CD=
AB·CD=![]() ,故④正确.
,故④正确.
∵Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,
∴CE=![]() AB=BE≠BC,故①错误;
AB=BE≠BC,故①错误;
∵∠ACB=90°,CD是斜边AB上的高,
∠A+∠B =90°,∠DCB+∠B =90°,
∴∠A=∠DCB,故②正确;
∵∠A+∠ACD=90°,
∴∠ACD=∠B,
∵CE=BE,
∴∠BCE=∠B,
∴∠ACD=∠BCE,故③正确;
∵CD⊥AB,且CE=![]() AB,
AB,
∴![]() =
=![]() AB·CD=
AB·CD=![]() ,故④正确,
,故④正确,
故答案为:②③④.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目