题目内容
根据如图中箭头的指向规律，从2013到2014再到2015，箭头的方向是以下图示中的（ ）
A、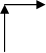 | B、 | C、 | D、 |
考点：规律型：数字的变化类
专题：规律型
分析：观察不难发现，每4个数为一个循环组依次循环，用2013除以4，根据商和余数的情况解答即可．
解答：解：由图可知，每4个数为一个循环组依次循环，2012÷4=503，
即0到2011共2012个数，构成前面503个循环，
∴2012是第504个循环的第1个数，2013是第504个循环组的第2个数，
∴从2013到2014再到2015，箭头的方向是．
故选：D．
即0到2011共2012个数，构成前面503个循环，
∴2012是第504个循环的第1个数，2013是第504个循环组的第2个数，
∴从2013到2014再到2015，箭头的方向是
．故选：D．
点评：本题是对数字变化规律的考查，仔细观察图形，发现每4个数为一个循环组依次循环是解题的关键．
练习册系列答案
相关题目
将1.24×10-3用小数表示为（ ）
| A、0.000124 | B、0.00124 | C、-0.00124 | D、0.0124 |
a、b经过运算后得到的结果如下表所示：
下列可以得到上述运算结果的算式是（ ）
| a | 0.5 | 0.25 |
| b | 2 | 4 |
| 运算结果 | 4 | 16 |
| A、ab-1 |
| B、a-1b |
| C、ab |
| D、（ab）2 |
下列各式计算错误的是（ ）
| A、a2b-3ab2=-2ab | B、x+2x=3x | C、a2b+a2b=2a2b | D、a2•a3=a5 |
a+b=-3，c+d=2，则（c-b）-（a-d）的值为（ ）
| A、5 | B、-5 | C、1 | D、-1 |
若一列不全为零的数除了第一个数和最后一个数外，每个数都等于前后与它相邻的两数之和，则称这列数具有“波动性质”．已知一列数共有18个，且具有“波动性质”，则这18个数的和为（ ）
| A、-64 | B、0 | C、18 | D、64 |
一列数a1，a2，a3，…，其中a1=1．an=
（n为大于1的整数），则a4等于（ ）
| 1 |
| 1+an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，M、N是正五边形ABCDE各边上的两个动点，若它们分别从顶点A、D出发，同时沿正六方形的边移动，M点以顺时针方向移动，N点以逆时针方向移动，假设点M的速度是点N的速度的5倍，则它们2012次相遇在（ ）边上．| A、AE | B、ED | C、CD | D、BC |
某商场购进一批服装，每件进价为200元，由于换季滞销，商场决定将这种服装按标价的六折销售，若打折后每件服装仍能获利20%，则该服装标价是（ ）
| A、350元 | B、400元 | C、450元 | D、500元 |