ΧβΡΩΡΎ»ί
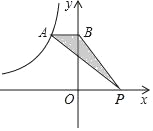
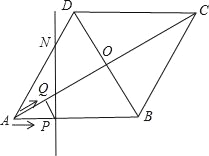
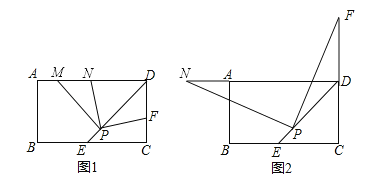
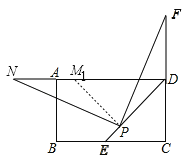
ΓΨΧβΡΩΓΩΨΊ–ΈABCD÷–Θ§DEΤΫΖ÷ΓœADCΫΜBC±Ώ”ΎΒψEΘ§PΈΣDE…œΒΡ“ΜΒψΘ®PEΘΦPDΘ©Θ§PMΓΆPDΘ§PMΫΜAD±Ώ”ΎΒψMΘ°
Θ®1Θ©»τΒψF «±ΏCD…œ“ΜΒψΘ§¬ζΉψPFΓΆPNΘ§«“ΒψNΈΜ”ΎAD±Ώ…œΘ§»γΆΦ1Υυ ΨΘ°
«σ÷ΛΘΚΔΌPN=PFΘΜΔΎDF+DN=![]() DPΘΜ
DPΘΜ
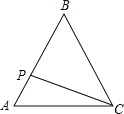
Θ®2Θ©»γΆΦ2Υυ ΨΘ§Β±ΒψF‘ΎCD±ΏΒΡ―”≥ΛœΏ…œ ±Θ§»‘»Μ¬ζΉψPFΓΆPNΘ§¥Υ ±ΒψNΈΜ”ΎDA±ΏΒΡ―”≥ΛœΏ…œΘ§»γΆΦ2Υυ ΨΘΜ ‘Έ DFΘ§DNΘ§DP”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§≤ΔΦ”“‘÷ΛΟςΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘ®2Θ©![]()
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©ΔΌάϊ”ΟΨΊ–ΈΒΡ–‘÷ Θ§ΫαΚœ“―÷ΣΧθΦΰΩ…÷ΛΓςPMNΓ’ΓςPDFΘ§‘ρΩ…÷ΛΒΟΫα¬έΘΜΔΎ”…Ι¥Ι…Ε®άμΩ…«σΒΟDM=![]() DPΘ§άϊ”ΟΔΌΩ…«σΒΟMN=DFΘ§‘ρΩ…÷ΛΒΟΫα¬έΘΜ
DPΘ§άϊ”ΟΔΌΩ…«σΒΟMN=DFΘ§‘ρΩ…÷ΛΒΟΫα¬έΘΜ
Θ®2Θ©ΙΐΒψPΉςPM1ΓΆPDΘ§PM1ΫΜAD±Ώ”ΎΒψM1Θ§‘ρΩ…÷ΛΒΟΓςPM1NΓ’ΓςPDFΘ§‘ρΩ…÷ΛΒΟM1N=DFΘ§Ά§Θ®1Θ©ΔΎΒΡΖΫΖ®Ω…÷ΛΒΟΫα¬έΘ°
œξΫβΘΚΘ®1Θ©ΔΌΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§ΓύΓœADC=90ΓψΘ°
”÷ΓΏDEΤΫΖ÷ΓœADCΘ§ΓύΓœADE=ΓœEDC=45ΓψΘΜ
ΓΏPMΓΆPDΘ§ΓœDMP=45ΓψΘ§ΓύDP=MPΘ°
ΓΏPMΓΆPDΘ§PFΓΆPNΘ§ΓύΓœMPN+ΓœNPD=ΓœNPD+ΓœDPF=90ΓψΘ§ΓύΓœMPN=ΓœDPFΘ°
‘ΎΓςPMNΚΆΓςPDF÷–Θ§ΓΏ 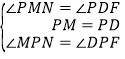 Θ§
Θ§
ΓύΓςPMNΓ’ΓςPDFΘ®ASAΘ©Θ§ΓύPN=PFΘ§MN=DFΘΜ
ΔΎΓΏPMΓΆPDΘ§DP=MPΘ§ΓύDM2=DP2+MP2=2DP2Θ§ΓύDM=![]() DPΘ°
DPΘ°
ΓΏ”÷ΓΏDM=DN+MNΘ§«“”…ΔΌΩ…ΒΟMN=DFΘ§ΓύDM=DN+DFΘ§ΓύDF+DN=![]() DPΘΜ
DPΘΜ
Θ®2Θ©![]() Θ°άμ”…»γœ¬ΘΚ
Θ°άμ”…»γœ¬ΘΚ
ΙΐΒψPΉςPM1ΓΆPDΘ§PM1ΫΜAD±Ώ”ΎΒψM1Θ§»γΆΦΘ§
ΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§ΓύΓœADC=90ΓψΘ°
”÷ΓΏDEΤΫΖ÷ΓœADCΘ§ΓύΓœADE=ΓœEDC=45ΓψΘΜ
ΓΏPM1ΓΆPDΘ§ΓœDM1P=45ΓψΘ§ΓύDP=M1PΘ§ΓύΓœPDF=ΓœPM1N=135ΓψΘ§Ά§Θ®1Θ©Ω…÷ΣΓœM1PN=ΓœDPFΘ°‘ΎΓςPM1NΚΆΓςPDF÷–Θ§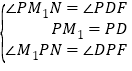 Θ§
Θ§
ΓύΓςPM1NΓ’ΓςPDFΘ®ASAΘ©Θ§ΓύM1N=DFΘ§”…Ι¥Ι…Ε®άμΩ…ΒΟΘΚ![]() =DP2+M1P2=2DP2Θ§ΓύDM1
=DP2+M1P2=2DP2Θ§ΓύDM1![]() DPΘ°
DPΘ°
ΓΏDM1=DN©¹M1NΘ§M1N=DFΘ§ΓύDM1=DN©¹DF![]() DPΘ°
DPΘ°

 ΩΎΥψ–ΓΉ¥‘ΣΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΩΎΥψ–ΓΉ¥‘ΣΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ ΧλΧλΝΖΩΎΥψœΒΝ–¥πΑΗ
ΧλΧλΝΖΩΎΥψœΒΝ–¥πΑΗ