题目内容
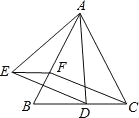
【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由△ABC是等边三角形得到∠B=60°,而∠EFB=60°,由此可以证明EF∥DC,而DC=EF,然后即可证明四边形EFCD是平行四边形;
(2)如图,连接BE,由BF=EF,∠EFB=60°可以推出△EFB是等边三角形,然后得到EB=EF,∠EBF=60°,而DC=EF,由此得到EB=DC,又
△ABC是等边三角形,所以得到∠ACB=60°,AB=AC,然后即可证明△AEB≌△ADC,利用全等三角形的性质就证明AE=AD.
试题解析:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC(内错角相等,两直线平行),
∵DC=EF,
∴四边形EFCD是平行四边形;
(2)连接BE
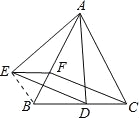
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠EBF=60°
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠EBF=∠ACB,
∴△AEB≌△ADC,
∴AE=AD.

【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?