题目内容
【题目】在一个边长为a(单位:cm)的正方形ABCD中,点E、M分别是线段AC、CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N

(1) 如图①,当点M与点C重合,求证:DF=MN;
(2) 如图②,假设点M从点C出发,以1 cm/s的速度沿CD向点D运动,点E同时从点A出发,以![]() cm/s速度沿AC向点C运动,运动时间为t(t>0)
cm/s速度沿AC向点C运动,运动时间为t(t>0)
① 判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
② 连结FM、FN,△MNF能否为等腰三角形?若能,请写出a、t之间的关系;若不能,请说明理由
【答案】(1)证明见解析;(2)①该命题是真命题.理由见解析;②能.理由见解析;
【解析】
试题分析:(1)证明△ADF≌△DNC,即可得到DF=MN;
(2)①首先证明△AFE∽△CDE,利用比例式求出时间t=![]() a,进而得到CM=
a,进而得到CM=![]() a=
a=![]() CD,所以该命题为真命题;
CD,所以该命题为真命题;
②若△MNF为等腰三角形,则可能有三种情形,需要分类讨论.
试题解析:(1)∵∠DNC+∠ADF=90°,∠DNC+∠DCN=90°,
∴∠ADF=∠DCN.
在△ADF与△DNC中,
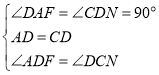 ,
,
∴△ADF≌△DNC(ASA),
∴DF=MN.
(2)①该命题是真命题.
理由如下:当点F是边AB中点时,则AF=![]() AB=
AB=![]() CD.
CD.
∵AB∥CD,∴△AFE∽△CDE,
∴![]() ,
,
∴AE=![]() EC,则AE=
EC,则AE=![]() AC=
AC=![]() a,
a,
∴t=![]() =
=![]() a.
a.
则CM=1![]() t=
t=![]() a=
a=![]() CD,
CD,
∴点M为边CD的三等分点.
②能.理由如下:
易证△AFE∽△CDE,∴![]() ,即
,即![]() ,得AF=
,得AF=![]() .
.
易证△MND∽△DFA,∴![]() ,即
,即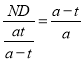 ,得ND=t.
,得ND=t.
∴ND=CM=t,AN=DM=a-t.
若△MNF为等腰三角形,则可能有三种情形:
(Ⅰ)若FN=MN,则由AN=DM知△FAN≌△NDM,
∴AF=ND,即![]() =t,得t=0,不合题意.
=t,得t=0,不合题意.
∴此种情形不存在;
(Ⅱ)若FN=FM,由MN⊥DF知,HN=HM,∴DN=DM=MC,
∴t=![]() a,此时点F与点B重合;
a,此时点F与点B重合;
(Ⅲ)若FM=MN,显然此时点F在BC边上,如下图所示:
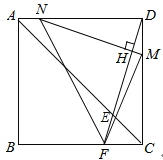
∵AN=DM,AD=CD,
∴ND=CM,
∵![]() ,
,
∴△MFC≌△NMD,∴FC=DM=a-t;
又由△NDM∽△DCF,∴![]() ,即
,即![]() ,∴FC=
,∴FC=![]() .
.
∴![]() =a-t,
=a-t,
∴t=a,此时点F与点C重合.
综上所述,当t=a或t=![]() a时,△MNF能够成为等腰三角形.
a时,△MNF能够成为等腰三角形.

 考前必练系列答案
考前必练系列答案