题目内容
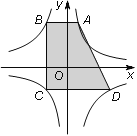
【题目】如图，A、C为反比例函数
上两点，B、D为反比例函数
上两点，且AB⊥
轴，BC⊥
轴，CD⊥
轴，点A的横坐标为
(
>0)．
（1）试用
直接表示点A、B、C、D的坐标．
（2）求四边形ABCD的边长和面积．
【答案】（1）A(
， 
)，B(
， 
)，C(
， 
)，D(
， 
)
（2）四边形ABCD的各边长为AB＝
，BC＝
，CD＝
，DA＝
，面积为
【解析】分析：（1）因为点A、B的纵坐标相同，B、C的横坐标相同，C、D的纵坐标相同，由点A的横坐标为a,分别代入y=
和y=
即可求解.(2)由A、B、C、D的坐标，可求出四边形的的边长，利用梯形面积公式即可求出四边形面积.
本题解析：（1）A(
， 
)，B(
， 
)，C(
， 
)，D(
， 
)．
（2）AB＝
，BC＝
，CD＝
，DA＝
．
．
练习册系列答案
金钥匙试卷系列答案
相关题目
【题目】根据下表中二次函数y=ax2+bx+c（a≠0）的对应值：
x | 3.23 | 3.24 | 3.25 | 3.26 |
y | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c=0（a≠0）的一个解x的范围是（ ）
A. 3.23＜x＜3.24 B. 3.24＜x＜3.25 C. 3.25＜x＜3.26 D. 不能确定
