题目内容
【题目】如图,P是AB为直径的半圆周上一点,点C在∠PAB的平分线上,且CB⊥AB于B,PB交AC于E,若AB=4,BE=2,则PE的长为 . 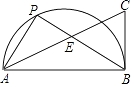
【答案】![]()
【解析】解:∵∠PAE=∠CAB,∠CAB+∠C=∠PAE+∠PEA,
∴∠PEA=∠C.
∵∠PEA=∠CEB,
∴∠C=∠CEB,
∴CB=BE=2= ![]() AB.
AB.
设PE=x,PA=2x.
(x+2)2+(2x)2=16,
解得:x= ![]() 或﹣2(舍去).
或﹣2(舍去).
则PE= ![]() .
.
故答案是: ![]() .
.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目
【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A | B | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?