题目内容
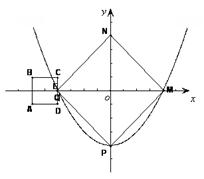
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A、D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O).

(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.

(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.
(1)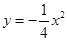 ;(2)①过点P作PG⊥y轴,垂足为G,由题意可知:F(0,-1),G(0,b),R(a,1),则
;(2)①过点P作PG⊥y轴,垂足为G,由题意可知:F(0,-1),G(0,b),R(a,1),则 ,
,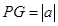 ,
, ,根据点P(a,b)为抛物线
,根据点P(a,b)为抛物线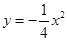 上的动点可得
上的动点可得 ,变形得:
,变形得: ,在Rt△PGF中,根据勾股定理即可证得结论;②存在,(
,在Rt△PGF中,根据勾股定理即可证得结论;②存在,(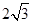 ,-3),(
,-3),(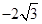 ,-3);③直角三角形
,-3);③直角三角形
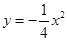 ;(2)①过点P作PG⊥y轴,垂足为G,由题意可知:F(0,-1),G(0,b),R(a,1),则
;(2)①过点P作PG⊥y轴,垂足为G,由题意可知:F(0,-1),G(0,b),R(a,1),则 ,
,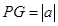 ,
, ,根据点P(a,b)为抛物线
,根据点P(a,b)为抛物线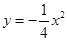 上的动点可得
上的动点可得 ,变形得:
,变形得: ,在Rt△PGF中,根据勾股定理即可证得结论;②存在,(
,在Rt△PGF中,根据勾股定理即可证得结论;②存在,(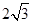 ,-3),(
,-3),(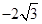 ,-3);③直角三角形
,-3);③直角三角形试题分析:(1)由题意可得点A的坐标为(2,-1),根据抛物线的顶点为坐标原点O可设抛物线的解析式为
 ,再将点A(2,-1)代入即可求得结果;
,再将点A(2,-1)代入即可求得结果;(2)①过点P作PG⊥y轴,垂足为G,由题意可知:F(0,-1),G(0,b),R(a,1),则
 ,
,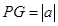 ,
, ,根据点P(a,b)为抛物线
,根据点P(a,b)为抛物线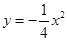 上的动点可得
上的动点可得 ,变形得:
,变形得: ,在Rt△PGF中,根据勾股定理即可证得结论;
,在Rt△PGF中,根据勾股定理即可证得结论;②由P(a,b),F(0,-1),R(a,1),根据勾股定理可表示出RF的长,由①可知:PF=PR=1-b,则可得当
 时△PFR为等边三角形,从而可以求得结果;
时△PFR为等边三角形,从而可以求得结果;③连接SF、RF,由PF=PR;PR∥FO可得∠1=∠2,∠1=∠3,即得
 ,同理可得
,同理可得 ,则
,则 ,即可得到结果.
,即可得到结果.(1)由题意可得:点A的坐标为(2,-1)
∵抛物线的顶点为坐标原点O
∴可设抛物线的解析式为:
 ;
;将点A(2,-1)代入可得:
 ;解得
;解得 ,
,∴抛物线的解析式为:
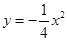 ;
;(2)①过点P作PG⊥y轴,垂足为G
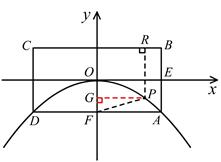
由题意可知:F(0,-1),G(0,b),R(a,1)
∴
 ,
,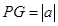 ,
,
∵点P(a,b)为抛物线
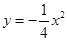 上的动点
上的动点∴
 ,变形得:
,变形得:
在Rt△PGF中,由勾股定理可得:
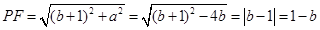
∴PF=PR;
②存在点P,使得△PFR为等边三角形;
∵P(a,b),F(0,-1),R(a,1)
∴
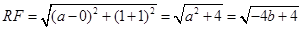
由①可知:PF=PR=1-b
∴当
 时△PFR为等边三角形
时△PFR为等边三角形解得:
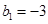 ,
,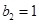 (不合题意,舍去)
(不合题意,舍去)∴当
 时,有
时,有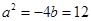 ,解得:
,解得: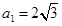 ,
,
∴点P的坐标为(
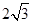 ,-3),(
,-3),(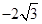 ,-3);
,-3);③△RSF为直角三角形.
如图,连接SF、RF

∵PF=PR;PR∥FO
∴∠1=∠2;∠1=∠3
∴

同理可得:

∴
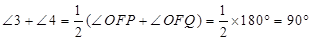
∴△RSF为直角三角形.
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
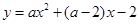 过点
过点 .
. 下方的部分沿直线
下方的部分沿直线 .点
.点 在图象
在图象 .
. 的取值范围;
的取值范围; 也在图象
也在图象 恒成立,则
恒成立,则 的取值范围为 .
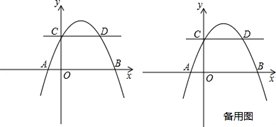
的取值范围为 . x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=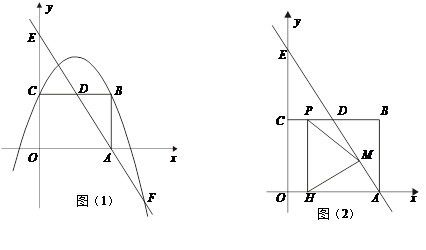
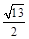 个单位长度的速度向终点E运动.过
个单位长度的速度向终点E运动.过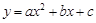 ,使它同时具有如下性质:
,使它同时具有如下性质: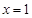 对称;②当x=2时,y>0;③当x=-2时,y<0.
对称;②当x=2时,y>0;③当x=-2时,y<0.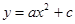 ,
,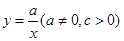 图象的是
图象的是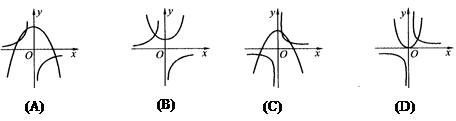
 配方后为
配方后为 ,则
,则 的值分别为( )
的值分别为( )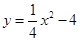 交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。