题目内容
【题目】如图,四边形OABC的四个顶点坐标分别为O(0,0),A(8,0),B(4,4),C(0,4),直线l:y=x+b保持与四边形OABC的边交于点M、N(M在折线AOC上,N在折线ABC上).设四边形OABC在l右下方部分的面积为S1 , 在l左上方部分的面积为S2 , 记S为S1、S2的差(S≥0).
(1)求∠OAB的大小;
(2)当M、N重合时,求l的解析式;
(3)当b≤0时,问线段AB上是否存在点N使得S=0?若存在,求b的值;若不存在,请说明理由;
(4)求S与b的函数关系式.
【答案】
(1)
解:过点B过BE⊥x轴,垂足为E.点E(4,0),
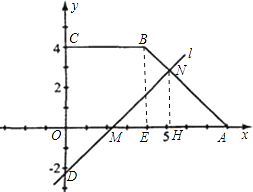
∴BE=4,AE=4,
∴△ABE为等腰直角三角形,
∴∠OAB=45°,
答:∠OAB=45°.
(2)
解:当点M、N重合到点C(0,4),
把C(0,4)代入y=x+b得:b=4,
∴直线l的解析式y=x+4;
当点M、N重合到点A(8,0)时,把(8,0)带入y=x+b得b=﹣8,
∴直线l的解析式为y=x﹣8.
(3)
解:四边形OABC的面积为 ![]() ×4(4+8)=24,
×4(4+8)=24,
直线l:y=x+b与x轴的交角为45°,△AMN为等腰直角三角形.
当S=0时,△AMN的面积为四边形OABC的面积的一半,即12.
过点N作x轴的垂线NH,
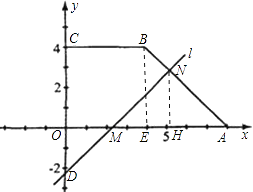
则NH=AH=MH,
设NH=a,
![]() ×2a×a=12,
×2a×a=12,
解得:a=2 ![]() ,
,
∴OH=8﹣2 ![]() ,
,
∴点N的坐标为(8﹣2 ![]() ,2
,2 ![]() ),
),
代入y=x+b得:b=4 ![]() ﹣8.
﹣8.
答:当b≤0时,线段AB上存在点N使得S=0,b的值是4 ![]() ﹣8.
﹣8.
(4)
解:分为三种情况:
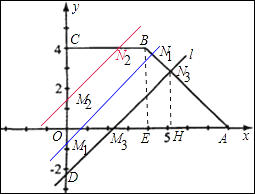
①如图在N1、M1时,当4 ![]() ﹣8≤b<0时,
﹣8≤b<0时,
OM=﹣b,AM=8﹣(﹣b)=8+b,
设直线AB的解析式是y=cx+d,
把A(8,0),B(4,4)代入得: ![]() ,
,
解得: ![]() ,
,
y=﹣x+8,
解方程组 ![]() 得:
得: 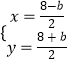 ,
,
S1= ![]() AM×NH=
AM×NH= ![]() ×2×
×2× ![]() ×
× ![]() =
= ![]() b2+4b+16;
b2+4b+16;
S2=24﹣S1,4
S=|S1﹣S2|= ![]() b2+4b+16﹣[24﹣(
b2+4b+16﹣[24﹣( ![]() b2+4b+16)]=
b2+4b+16)]= ![]() b2+8b+8,
b2+8b+8,
②当0≤b≤4时,如图在N2、M2点时,OM=b,CM=4﹣b,
S2= ![]() (4﹣b)2,S1=24﹣S2,
(4﹣b)2,S1=24﹣S2,
S=S1﹣S2=﹣b2+8b+8,
③﹣8<a<﹣8+4 ![]() 时,如图,在N3、M3时,S1=
时,如图,在N3、M3时,S1= ![]() ×2×
×2× ![]() ×
× ![]() =
= ![]() b2+4b+16;
b2+4b+16;
S2=24﹣S1,
S=S2﹣S1=[24﹣( ![]() b2+4b+16)]﹣(
b2+4b+16)]﹣( ![]() b2+4b+16)=﹣
b2+4b+16)=﹣ ![]() b2+8b+8.
b2+8b+8.
综上可得,S=  .
.
【解析】(1)过点B过BE⊥x轴,垂足为E.求出点E的坐标,求出等腰直角三角形ABE即可;(2)把A(8,0)C(0,4)点代入y=x+b求出即可;(3)求出梯形的面积,过点N作x轴的垂线NH,得到NH=AH=MH,设NH=a,代入面积公式求出a,代入解析式求出b即可;(4)分为三种情况:①当0≤b≤4时,②当4 ![]() ﹣8≤b<0时,③③﹣8<a<﹣8+4
﹣8≤b<0时,③③﹣8<a<﹣8+4 ![]() 时,设直线AB的解析式是y=cx+d,把A(8,0),B(4,4)代入求出解析式,解两直线组成的方程组,求出交点坐标,根据梯形和三角形的面积求出S即可.
时,设直线AB的解析式是y=cx+d,把A(8,0),B(4,4)代入求出解析式,解两直线组成的方程组,求出交点坐标,根据梯形和三角形的面积求出S即可.
【考点精析】掌握一次函数的图象和性质是解答本题的根本,需要知道一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小
明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包
贴时没有重叠部分). 小明通过操作后发现此类包贴问题可将直三棱柱的
侧面展开进行分析.


(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是cm.









