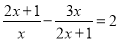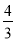题目内容
如图,已知∠MON两边分别为OM、ON,sin∠O= 且OA=5,点D为线段OA上的动点(不与O重合),以A为圆心、AD为半径作⊙A,设OD=x.
且OA=5,点D为线段OA上的动点(不与O重合),以A为圆心、AD为半径作⊙A,设OD=x.

(1)若⊙A交∠O 的边OM于B、C两点,BC=y,求y关于x的函数解析式,并写出函数的定义域;
(2)将⊙A沿直线OM翻折后得到⊙A′.
①若⊙A′与直线OA相切,求x的值;
②若⊙A′与以D为圆心、DO为半径的⊙D相切,求x的值.
(1)y=2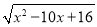 (0<x<5);(2)①x=
(0<x<5);(2)①x=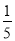 ;②
;②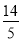 .
.
【解析】
试题分析:(1)作AH⊥OM于H,如图1,在Rt△OAH中,根据正弦的定义求出AH=3,根据垂径定理由AH⊥BC得CH=BH=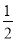 BC=
BC=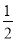 y,由于OD=x,则AD=5-x,然后在Rt△ACH中利用勾股定理得到(
y,由于OD=x,则AD=5-x,然后在Rt△ACH中利用勾股定理得到(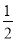 y)2=(5-x)2-32,再整理即可得到y与x的函数关系;
y)2=(5-x)2-32,再整理即可得到y与x的函数关系;
(2)①作A′E⊥OA于E,根据折叠的性质得A′H=AH=3,⊙A′的半径为5-x,在Rt△OAH中,利用勾股定理计算出OH=4;由于⊙A′与直线OA相切,根据切线的性质得A′E=5-x,再证明Rt△OAH∽Rt△A′AE,利用相似比得到5:6=4:(5-x),然后解方程可得到x的值;
②作A′G⊥OA于G,连结A′D,根据两圆相切的性质得A′D=x+5-x=5,再证明Rt△OAH∽Rt△A′AG,利用相似比可计算出AG=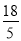 ,A′G=
,A′G=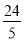 ,则DG=AG-AD=x-
,则DG=AG-AD=x-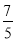 ,然后在Rt△A′GD中,根据勾股定理得到(
,然后在Rt△A′GD中,根据勾股定理得到(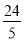 )2+(x-
)2+(x-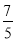 )2=52,整理得x2-
)2=52,整理得x2-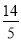 x=0,然后解方程即可.
x=0,然后解方程即可.
试题解析:(1)作AH⊥OM于H,如图1,
在Rt△OAH中,OA=5,sin∠AOH=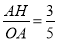 ,
,
∴AH=3,
∵AH⊥BC,
∴CH=BH=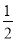 BC=
BC=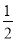 y,
y,
∵OD=x,
∴AD=5-x,
在Rt△ACH中,AC=5-x,AH=3,CH=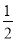 y,
y,
∴(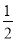 y)2=(5-x)2-32,
y)2=(5-x)2-32,
∴y=2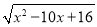 (0<x<5);
(0<x<5);
(2)①作A′E⊥OA于E,如图,
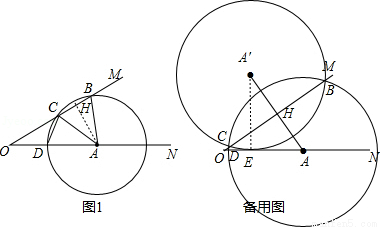
∵⊙A沿直线OM翻折后得到⊙A′,
∴A′H=AH=3,⊙A′的半径为5-x,
在Rt△OAH中,OH=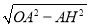 =4,
=4,
∵⊙A′与直线OA相切,
∴A′E=5-x,
∵∠HAO=∠EAA′,
∴Rt△OAH∽Rt△A′AE,
∴OA:AA′=OH:A′E,即5:6=4:(5-x),
∴x=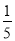 ;
;
②作A′G⊥OA于G,连结A′D,如图3,
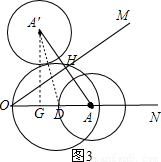
∵⊙A′与以D为圆心、DO为半径的⊙D相切,
∴A′D=x+5-x=5,
∵∠HAO=∠GAA′,
∴Rt△OAH∽Rt△A′AG,
∴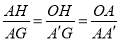 ,即
,即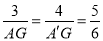 ,
,
∴AG=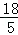 ,A′G=
,A′G=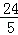 ,
,
∴DG=AG-AD=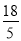 -(5-x)=x-
-(5-x)=x-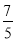 ,
,
在Rt△A′GD中,∵A′G2+GD2=A′D2,
∴(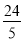 )2+(x-
)2+(x-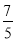 )2=52,
)2=52,
整理得x2-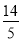 x=0,解得x1=0(舍去),x2=
x=0,解得x1=0(舍去),x2=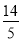 ,
,
∴x的值为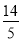 .
.
考点:圆的综合题.

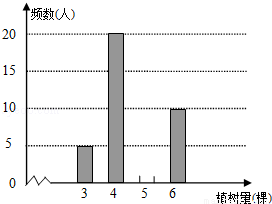
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
植树数量(棵) | 频数(人) | 频率
|
3 | 5 | 0.1 |
4 | 20 | 0.4 |
5 |
|
|
6 | 10 | 0.2 |
合计 | 50 | 1 |
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数,并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量.