题目内容
阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2.例如:x2-2x+4=x2-2x+1+3=(x-1)2+3是x2-2x+4的一种形式的配方,x2-2x+4=x2-4x+4+2x=(x-2)2+2x是x2-2x+4的另一种形式的配方…
请根据阅读材料解决下列问题:
(1)比照上面的例子,写出x2-4x+1的两种不同形式的配方;
(2)已知x2+y2-4x+6y+13=0,求2x-y的值;
(3)已知a2+b2+c2-ab-3b-2c+4=0,求a+b+c的值.
解:(1)x2-4x+2的三种配方分别为:
x2-4x+1=(x-2)2-3,
x2-4x+1=(x-1)2-2x,
(2)由x2+y2-4x+6y+13=0得:x2-4x+4+y2+6y+9=0,
∴(x-2)2+(y+3)2=0
解得:x=2,y=-3
∴2x-y=4+3=7;
(3)a2+b2+c2-ab-3b-2c+4
=(a2-ab+ b2)+(
b2)+( b2-3b+3)+(c2-2c+1)
b2-3b+3)+(c2-2c+1)
=(a2-ab+ b2)+
b2)+ (b2-4b+4)+(c2-2c+1)
(b2-4b+4)+(c2-2c+1)
=(a- b)2+
b)2+ (b-2)2+(c-1)2=0,
(b-2)2+(c-1)2=0,
从而有a- b=0,b-2=0,c-1=0,
b=0,b-2=0,c-1=0,
即a=1,b=2,c=1,
故a+b+c=4.
分析:(1)由题中所给的已知材料可得x2-4x+1和a2+ab+b2的配方也可分别常数项、一次项、二次项两种种不同形式;
(2)通过配方后,求得x,y的值,再代入代数式求值.
(3)通过配方后,求得a,b,c的值,再代入代数式求值.
点评:本题考查了根据完全平方公式:a2±2ab+b2=(a±b)2进行配方的能力.
x2-4x+1=(x-2)2-3,
x2-4x+1=(x-1)2-2x,
(2)由x2+y2-4x+6y+13=0得:x2-4x+4+y2+6y+9=0,
∴(x-2)2+(y+3)2=0
解得:x=2,y=-3
∴2x-y=4+3=7;
(3)a2+b2+c2-ab-3b-2c+4
=(a2-ab+
 b2)+(
b2)+( b2-3b+3)+(c2-2c+1)
b2-3b+3)+(c2-2c+1)=(a2-ab+
 b2)+
b2)+ (b2-4b+4)+(c2-2c+1)
(b2-4b+4)+(c2-2c+1)=(a-
 b)2+
b)2+ (b-2)2+(c-1)2=0,
(b-2)2+(c-1)2=0,从而有a-
 b=0,b-2=0,c-1=0,
b=0,b-2=0,c-1=0,即a=1,b=2,c=1,
故a+b+c=4.
分析:(1)由题中所给的已知材料可得x2-4x+1和a2+ab+b2的配方也可分别常数项、一次项、二次项两种种不同形式;
(2)通过配方后,求得x,y的值,再代入代数式求值.
(3)通过配方后,求得a,b,c的值,再代入代数式求值.
点评:本题考查了根据完全平方公式:a2±2ab+b2=(a±b)2进行配方的能力.

练习册系列答案
相关题目
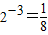 ,所以
,所以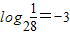 .
.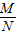 =______(a>0,a≠1,M、N均为正数).
=______(a>0,a≠1,M、N均为正数).