题目内容
阅读下面材料,并解答下列各题:在形如ab=N的式子中,我们已经研究过两种情况:
①已知a和b,求N,这是乘方运算;
②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算.
定义:如果ab=N(a>0,a≠1,N>0),则b叫做以a为底N的对数,记着b=logaN.
例如:因为23=8,所以log28=3;因为2-3=
| 1 |
| 8 |
| 1 |
| 8 |
(1)根据定义计算:
①log381=
④如果logx16=4,那么x=
(2)设ax=M,ay=N,则logaM=x,logaN=y(a>0,a≠1,M、N均为正数),
∵ax•ay=ax+y,∴ax+y=M•N∴logaMN=x+y,
即logaMN=logaM+logaN
这是对数运算的重要性质之一,进一步,我们还可以得出:
logaM1M2M3…Mn=
loga
| M |
| N |
分析:(1)根据题中给出的对数的运算的定义和法则计算即可;
(2)根据题中给出的对数运算法则总结即可得出下面两个式子的答案.
(2)根据题中给出的对数运算法则总结即可得出下面两个式子的答案.
解答:解:根据题中给出的已知条件可得:(1)①4,②1;③0;④2(每空1分,共4分)
(2)logaM1+logaM2+logaM3+logaMn
logaM-logaN(每空2分,共4分)
故答案为:(1)①4,②1;③0;④2;(2)logaM1+logaM2+logaM3+logaMn,logaM-logaN
(2)logaM1+logaM2+logaM3+logaMn
logaM-logaN(每空2分,共4分)
故答案为:(1)①4,②1;③0;④2;(2)logaM1+logaM2+logaM3+logaMn,logaM-logaN
点评:本题立意比较新颖,根据题中条件计算并且推算出对数运算的法则,考查了学生的举一反三的能力和对新知识的掌握,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ;
; ;
; .
. 的结果 ;
的结果 ; = ,此时称
= ,此时称 与
与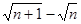 互为有理化因式;
互为有理化因式;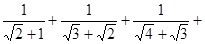 …+
…+  。
。