题目内容
如图，三角形纸片ABC中，∠A=70°，∠B=70°，将纸片的一角折叠，使点C落在△ABC内，若∠1=25°，则∠2的度数为55°
55°
．分析：根据三角形的内角和定理求出∠3+∠4=∠A+∠B，再根据翻折变换的性质列式求解即可．
解答：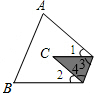
解：如图，∵∠A+∠B+∠C=180°，∠3+∠4+∠C=180°，
∴∠3+∠4=∠A+∠B=70°+70°=140°，
由翻折的性质，∠1+∠2=180°×2-2（∠3+∠4），
∵∠1=25°，
∴25°+∠2=360°-2×140°，
解得∠2=55°．
故答案为：55°．
解：如图，∵∠A+∠B+∠C=180°，∠3+∠4+∠C=180°，∴∠3+∠4=∠A+∠B=70°+70°=140°，
由翻折的性质，∠1+∠2=180°×2-2（∠3+∠4），
∵∠1=25°，
∴25°+∠2=360°-2×140°，
解得∠2=55°．
故答案为：55°．
点评：本题考查了三角形的内角和定理，翻折变换的性质，整体思想的利用是解题的关键是解题的关键．
练习册系列答案
相关题目
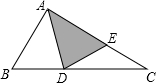（2012•南岗区三模）如图，三角形纸片ABC中，∠B=2∠C，把三角形纸片沿直线AD折叠，点B落在AC边上的E处，那么下列等式成立的是（ ）
如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（ ）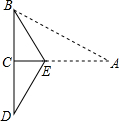
如图，三角形纸片ABC中，∠BCA=90°，∠A=30°，AB=6，在AC上取一点 E，沿BE 将该纸片折叠，使AB的一部分与BC重合，点A与BC延长线上的点D重合，求DE的长．
如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（ ）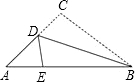
如图，三角形纸片ABC，AB=12cm，BC=7cm，AC=8cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（ ）