题目内容
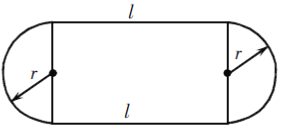
【题目】如图，操场的两端为半圆形，中间是一个长方形． 已知半圆的半径为r，直跑道的长为l，请用关于r，l的多项式表示这个操场的面积． 这个多项式能分解因式吗？若能，请把它分解因式，并计算当r＝40m，l＝30πm时操场的面积(结果保留π)；若不能，请说明理由．
【答案】πr2＋2rl；能分解因式；πr2＋2rl＝r(πr＋2l)；当r＝40m，l＝30πm时，操场的面积＝4000π(m2)．
【解析】
根据操场面积=圆的面积+长方形面积列式即可，然后提公因式分解，最后代入求值．
操场面积=圆的面积+长方形面积=πr2＋2rl= r(πr＋2l)．
当r=40m，l=30πm时，操场的面积=40×（40π+2×30π）=4000π(m2)．
练习册系列答案
阅读快车系列答案
相关题目
