Question

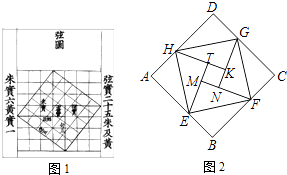
【题目】如图1，将一条两边互相平行的纸带折叠。

（1）若图中α=70,则β=°；
（2）探求图中α与β的数量关系；
（3）在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2)，若继续沿CB边折叠，CE边恰好平分∠ACB，直接写出此时β的大小。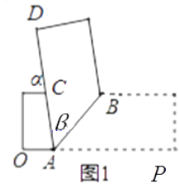

Answer 1

【答案】
（1）55
（2）

解：因为纸带两边平行，

所以∠OAC=α，

由折叠可得∠BAP=β，

由平角的定义可得∠OAC+β+∠BAP=180°，

即α+2β=180°，

则β=90°- .

（3）

解：由折叠可得2∠BCE=∠BCD（图1中）=180°-α=2β，即∠BCE=β.

而∠BCE= ∠ACB，所以∠ACB=2β.

因为纸带两边平行，

所以∠ACB+β=180°，

则3β=180°，

解得β=60°.

【解析】（1）因为纸带两边平行，
所以∠OAC=α，
由折叠可得∠BAP=β，
由平角的定义可得∠OAC+β+∠BAP=180°，
即α+2β=180°，
则β=90°- =55°.
所以答案是55.
【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．