题目内容
已知A1、A2、A3是抛物线y= x2上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.
x2上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.
(1)如图,若A1、A2、A3三点的横坐标依次为1,2,3,求线段CA2的长;
(2)如图,若将抛物线y= x2改为抛物线y=
x2改为抛物线y= x2﹣x+1,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长;
x2﹣x+1,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长;
(3)若将抛物线y= x2改为抛物线y=ax2+bx+c,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案).
x2改为抛物线y=ax2+bx+c,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案).
 x2上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.
x2上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C. (1)如图,若A1、A2、A3三点的横坐标依次为1,2,3,求线段CA2的长;
(2)如图,若将抛物线y=
 x2改为抛物线y=
x2改为抛物线y= x2﹣x+1,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长;
x2﹣x+1,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长; (3)若将抛物线y=
 x2改为抛物线y=ax2+bx+c,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案).
x2改为抛物线y=ax2+bx+c,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案).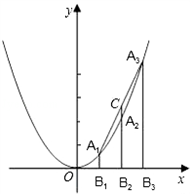
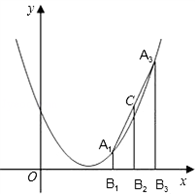
解:(1)方法一:∵A1、A2、A3三点的横坐标依次为1、2、3,
∴A1B1= ×12=
×12= ,A2B2=
,A2B2= ×22=2,A3B3=
×22=2,A3B3= ×32=
×32=
设直线A1A3的解析式为y=kx+b.
∴ 解得
解得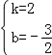
∴直线A1A3的解析式为y=2x﹣ ,
,
∴CB2=2×2﹣ =
=
∴CA2=CB2﹣A2B2= ﹣2=
﹣2= .
.
(2)方法一:设A1、A2、A3三点的横坐标依次为n﹣1、n、n+1,则A1B1= (n﹣1)2﹣(n﹣1)+1,A2B2=
(n﹣1)2﹣(n﹣1)+1,A2B2= n2﹣n+1,A3B3=
n2﹣n+1,A3B3= (n+1)2﹣(n+1)+1
(n+1)2﹣(n+1)+1
设直线A1A3的解析式为y=kx+b.
∴
解得 ,
,
∴直线A1A3的解析式为y=(n﹣1)x﹣ n2+
n2+ .
.
∴CB2=n(n﹣1)﹣ n2+
n2+ =
= n2﹣n+
n2﹣n+
∴CA2=CB2﹣A2B2= n2﹣n+
n2﹣n+ ﹣
﹣ n2+n﹣1=
n2+n﹣1=
(3)当a>0时,CA2=a;当a<0时,CA2=﹣a.
∴A1B1=
 ×12=
×12= ,A2B2=
,A2B2= ×22=2,A3B3=
×22=2,A3B3= ×32=
×32=
设直线A1A3的解析式为y=kx+b.
∴
 解得
解得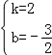
∴直线A1A3的解析式为y=2x﹣
 ,
,∴CB2=2×2﹣
 =
=
∴CA2=CB2﹣A2B2=
 ﹣2=
﹣2= .
.(2)方法一:设A1、A2、A3三点的横坐标依次为n﹣1、n、n+1,则A1B1=
 (n﹣1)2﹣(n﹣1)+1,A2B2=
(n﹣1)2﹣(n﹣1)+1,A2B2= n2﹣n+1,A3B3=
n2﹣n+1,A3B3= (n+1)2﹣(n+1)+1
(n+1)2﹣(n+1)+1设直线A1A3的解析式为y=kx+b.
∴

解得
 ,
,∴直线A1A3的解析式为y=(n﹣1)x﹣
 n2+
n2+ .
.∴CB2=n(n﹣1)﹣
 n2+
n2+ =
= n2﹣n+
n2﹣n+
∴CA2=CB2﹣A2B2=
 n2﹣n+
n2﹣n+ ﹣
﹣ n2+n﹣1=
n2+n﹣1=
(3)当a>0时,CA2=a;当a<0时,CA2=﹣a.

练习册系列答案
相关题目

 如图,已知A1,A2,A3,…,A2006是x轴上的点,且OA1=A1A2=A2A3=…=A2005A2006=1,分别过点A1,A2,A3,…,A2006作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2006点,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2005B2005P2006的面积为S2006,则S2006-S2005=
如图,已知A1,A2,A3,…,A2006是x轴上的点,且OA1=A1A2=A2A3=…=A2005A2006=1,分别过点A1,A2,A3,…,A2006作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2006点,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2005B2005P2006的面积为S2006,则S2006-S2005=