题目内容
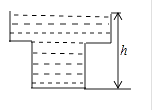
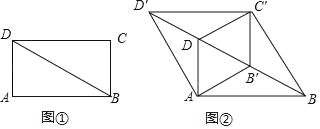
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
【答案】(1)证明见解析;(2)4![]() ;(3)矩形周长为6+
;(3)矩形周长为6+![]() 或2
或2![]() +3.
+3.
【解析】试题分析:(1)有一组邻边相等的平行四边形是菱形,据此进行证明即可;
(2)先判定四边形ABC'D'是菱形,再根据边长AB=![]() AD=
AD=![]() ,即可得到四边形ABC'D′的周长为4
,即可得到四边形ABC'D′的周长为4![]() ;
;
(3)根据两种不同的拼法,分别求得可能拼成的矩形周长.
试题解析:(1)∵BD是矩形ABCD的对角线,∠ABD=30°,
∴∠ADB=60°,
由平移可得,B'C'=BC=AD,∠D'B'C'=∠DBC=∠ADB=60°,
∴AD∥B'C'
∴四边形AB'C'D是平行四边形,
∵B'为BD中点,
∴Rt△ABD中,AB'=![]() BD=DB',
BD=DB',
又∵∠ADB=60°,
∴△ADB'是等边三角形,
∴AD=AB',
∴四边形AB'C'D是菱形;
(2)由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°,
∴AB∥C'D',
∴四边形ABC'D'是平行四边形,
由(1)可得,AC'⊥B'D,
∴四边形ABC'D'是菱形,
∵AB=![]() AD=
AD=![]() ,
,
∴四边形ABC'D′的周长为4![]() ,
,
故答案为:4![]() ;
;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形如下:
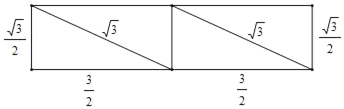
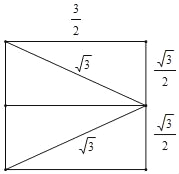
∴矩形周长为6+![]() 或2
或2![]() +3.
+3.

【题目】为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个) | 人数 |
0 | 1 |
1 | 2 |
2 | x |
3 | y |
4 | 4 |
5 | 2 |
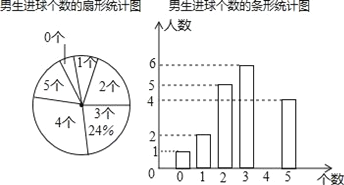
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有_____人.