Question

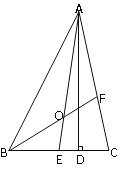
【题目】如图，在△OAB中，OA=OB，C为AB中点，以O圆心，OC长为半径作圆，AO与⊙O交于点E，直线OB与⊙O交于点F和D，连接EF、CF，CF与OA交于点G.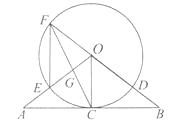

（1）求证：直线AB是⊙O的切线；
（2）求证：OD·EG=OG·EF；
（3）若AB=8，BD=2，求⊙O的半径.

Answer 1

【答案】
（1）

解：证明：∵OA=OB，C为AB中点，

∴OC⊥AB，

∴直线AB是⊙O的切线.

（2）

解：证明：∵OA=OB，C为AB中点，

∴∠AOC=∠BOC，

∴ ，

∴∠EFC=∠DFC，

∵OF=OC，

∴∠OFC=∠OCF，

∴∠EFC=∠OCF，

又∵∠EGF=∠OGC，

∴△EGF∽△OGC，

∴ ，

∵OD=OC，

∴ ，

∴ OD·EG=OG ·EF．

（3）

解：∵AB=8，C为AB中点，

∴BC=4，

设⊙O的半径为r，

∵在Rt△OCB中，OC2+BC2=OB2，

∴r2+42=(r+2)2，

解得：r=3，

∴⊙O 的半径为3．

【解析】（1）由等腰三角形的“三线合一”易得OC⊥AB，即直线AB是⊙O的切线；（2）要证OD·EG=OG·EF，就要证 ，而OD=OC，就要证 ，则要证△EGF∽△OGC，而∠EGF=∠OGC，只需要证∠EFC=∠OCF即可；（3）在Rt△OCB中，⊙O的半径为r，由勾股定理构造方程解答.