��Ŀ����
��ͼ1����ƽ��ֱ������ϵ�У���A��C�ֱ���y���x���ϣ�AB��x�ᣬsinC= ����P��O��������ر�OA��AB��BC�����˶�����Q�ӵ�C��������1cm/s���ٶ��ر�CO�����˶�����P���Qͬʱ����������һ�㵽���յ㣬��һ��Ҳ��ֹ֮ͣ�˶�.���P�˶���ʱ��Ϊt(s)����CPQ�����ΪS(cm2)�� ��֪S��t֮��ĺ�����ϵ��ͼ2�����߶�OE���߶�EF�����߶�FG������
����P��O��������ر�OA��AB��BC�����˶�����Q�ӵ�C��������1cm/s���ٶ��ر�CO�����˶�����P���Qͬʱ����������һ�㵽���յ㣬��һ��Ҳ��ֹ֮ͣ�˶�.���P�˶���ʱ��Ϊt(s)����CPQ�����ΪS(cm2)�� ��֪S��t֮��ĺ�����ϵ��ͼ2�����߶�OE���߶�EF�����߶�FG������
��1����P���˶��ٶ�Ϊ cm/s�� ��B��C������ֱ�Ϊ �� ��
��2��������FG�εĺ�������ʽ��
��3����tΪ��ֵʱ����CPQ��������ı���OABC�������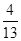 ��
��
�������������(1)����ͼ2֪����Q�˶�2��ʱ��CPQ�����Ϊ4cm2,�������������ʽ�������P���˶��ٶȣ���Q�˶�4.5��ʱ����CPQ������ﵽ���ʱOA+AB=9���Ӷ������B���A���꣬��sinC= �������C�����ꣻ
�������C�����ꣻ
�������ֶ������������ʽ��
������������ı���OABC��������ɡ�CPQ ��������ı���OABC�������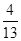 ���������t��ֵ.
���������t��ֵ.
�����������1��2,��5��4����(8��0)��
��2��i)��0��t��2ʱ��s=t2;
ii) ��2��t��4.5ʱ��s=2t��
iii) ��4.5��t��9ʱ�� ��
��
��3��t="4" ��t=5.
���㣺��̬��������.



 �����㣬���E��x��y������������һ���㣬����x���·����ı���OEBF����OBΪ�Խ��ߵ�ƽ���ı��Σ�
�����㣬���E��x��y������������һ���㣬����x���·����ı���OEBF����OBΪ�Խ��ߵ�ƽ���ı��Σ�
 =
= ����k��
����k��

 ��
�� ��m��0��m��
��m��0��m�� x2��bx��c������B���Ҷ�����ֱ��x��
x2��bx��c������B���Ҷ�����ֱ��x�� �ϣ�
�ϣ�
 ������
�У����� �ı�
�ı� ��
�� ���ϣ���
���ϣ��� ��
�� ��ֱ��
��ֱ�� ������
������ ����
���� ���ڵ�
���ڵ�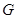 ��
�� ������ֱ���
������ֱ��� �������ߵĽ���ʽ��
�������ߵĽ���ʽ�� ������Ϊ��
��������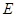 �������
������� ʱ�����ߵĽ���ʽ��
ʱ�����ߵĽ���ʽ��
 ��
�� �ύ��
�ύ�� ���㣬��
���㣬�� �ύ�ڵ�
�ύ�ڵ� ������AC����
������AC����
 ʱ�������
ʱ�������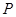 �����ꣻ
�����ꣻ ��
�� ���߶�
���߶� ��
�� �غϣ���һ������.����
�غϣ���һ������.���� �����������ڵ�
�����������ڵ� ������
������ ��
�� �����
����� ��������������Ϊ���٣�
��������������Ϊ���٣�
 ���룮
���룮