Question

【题目】如图，点O是直线AB上一点，∠BOC=120°，OD平分∠AOC．

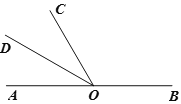
(1)求∠COD的度数．

请你补全下列解题过程．

∵点O为直线AB上一点，

∴∠AOB=_____．

∵∠BOC =120°，

∴∠AOC=______．

∵OD 平分∠AOC，

∴∠COD=∠AOC．( )

∴∠COD=________．

(2)若E是直线AB外一点，满足∠COE：∠BOE=4：1直接写出∠BOE的度数．

Answer 1

【答案】(1)180°；60°；角平分线定义；30°；(2)24°或40°.

【解析】

(1)利用∠BOC=120°及补角的性质就可求出∠AOC的度数，根据角平分线的定义就可求出∠COD的度数；

(2)分OE在∠BOC内部和OE在∠BOC外部两种情况进行计算.

解：(1)∵点O为直线AB上一点，

∴∠AOB= 180° ．

∵∠BOC =120°，

∴∠AOC= 60° ．

∵OD 平分∠AOC，

∴∠COD=∠AOC．(角平分线定义)

∴∠COD= 30° ；

(2)如图，当OE在∠BOC内部时，

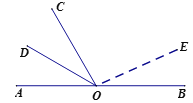
∵∠BOC=120°，∠COE:∠BOE=4:1，

∴∠BOE=∠BOC=24°；

如图，当OE在∠BOC外部时，

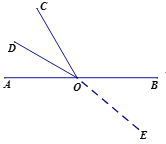
∵∠BOC=120°，∠COE:∠BOE=4:1，

∴=，

∴∠BOE=40°.

故答案为：(1)180°；60°；角平分线定义；30°；(2)24°或40°.