Question

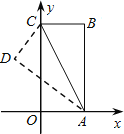
【题目】如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC
（1）求证：△ABD≌△ECB；
（2）若∠EDC=65°，求∠ECB的度数；
（3）若AD=3，AB=4，求DC的长．

Answer 1

【答案】
（1）证明：∵AD∥BC，

∴∠ADB=∠EBC，

∵∠A=∠CEB=90°，

在△ABD与△CEB中， ，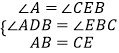

∴△ABD≌△ECB

（2）解：由（1）证得△ABD≌△ECB，

∴BD=BC，

∴∠BCD=∠BDC=65°，

∵∠DCE=90°﹣65°=25°，

∴∠ECB=40°

（3）解：由（1）证得△ABD≌△ECB，

∴CE=AB=4，BE=AB=3，

∴BD=BC= =5，

∴DE=2，

∴CD= =2

【解析】（1）由AD∥BC，得到∠ADB=∠EBC，又因为∠A=∠CEB=90°，推出△ABD≌△ECB；（2）根据等腰三角形的性质和直角三角形的性质得到结果；（3）由全等三角形的性质得到对应边相等，利用勾股定理解出结果．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．