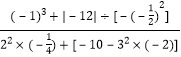题目内容
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
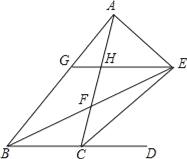
【答案】①③④.
【解析】
①根据角平分线的定义得到∠EBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACD,根据外角的性质即可得到结论;
∠ACD,根据外角的性质即可得到结论;
②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;
③由BG=GE,CH=EH,于是得到BG-CH=GE-EH=GH.即可得到结论;
④由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.
①BE平分∠ABC,
∴∠EBC=![]() ∠ABC,
∠ABC,
∵CE平分∠ACD,
∴∠DCE=![]() ∠ACD,
∠ACD,
∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,
∴∠EBC+∠BEC=![]() (∠BAC+∠ABC)=∠EBC+
(∠BAC+∠ABC)=∠EBC+![]() ∠BAC,
∠BAC,
∴∠BEC=![]() ∠BAC,故①正确;
∠BAC,故①正确;
∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所以不能得出全等的结论,故②错误;
③BE平分∠ABC,
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,
同理CH=HE,
∴BGCH=GEEH=GH,
∴BG=CH+GH,
故③正确;
④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,
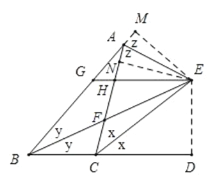
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,
则∠BAC=180![]() 2z,∠ACB=180
2z,∠ACB=180![]() 2x,
2x,
∵∠ABC+∠ACB+∠BAC=180![]() ,
,
∴2y+180![]() 2z+180
2z+180![]() 2x=180
2x=180![]() ,
,
∴x+z=y+90![]() ,
,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90![]() ,
,
∴x+∠AEB=90![]() ,
,
即∠ACE+∠AEB=90![]() ,
,
故④正确.
故答案为:①③④.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案