题目内容
【题目】如图,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式.
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标.
(3)在第二问的条件下,射线DE上是否存在点P,使得以C、D、P为顶点的三角形与△DOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=x2﹣2x﹣3;(2)(0,﹣1);(3)满足条件的点P共有2个,其坐标分别为(![]() ,﹣2)、(3,﹣10).
,﹣2)、(3,﹣10).
【解析】
试题(1)把点A、B的坐标代入抛物线解析式,解方程组求出b、c的值,即可得解;
(2)令y=0,利用抛物线解析式求出点C的坐标,设点D的坐标为(0,m),作EF⊥y轴于点F,利用勾股定理列式表示出DC2与DE2,然后解方程求出m的值,即可得到点D的坐标;
(3)根据点C、D、E的坐标判定△COD和△DFE全等,根据全等三角形对应角相等可得∠EDF=∠DCO,然后求出CD⊥DE,再利用勾股定理求出CD的长度,然后①分OC与CD是对应边;②OC与DP是对应边;根据相似三角形对应边成比例列式求出DP的长度,过点P作PG⊥y轴于点G,分别求出DG、PG的长度,结合平面直角坐标系即可写出点P的坐标.
试题解析:
(1)∵抛物线y=x2+bx+c经过A(﹣1,0)、B(0,﹣3),
∴![]() ,
,
解得![]() ,
,
故抛物线的函数解析式为y=x2﹣2x﹣3;
(2)令x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
则点C的坐标为(3,0),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴点E坐标为(1,﹣4),
设点D的坐标为(0,m),
∵DC2=OD2+OC2=m2+32,DE2=DF2+EF2=(m+4)2+12,
∵DC=DE,
∴m2+9=m2+8m+16+1,
解得m=﹣1,
∴点D的坐标为(0,﹣1);
(3)作EF⊥y轴于F.
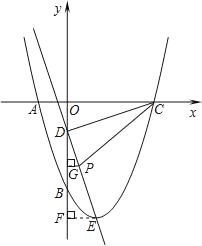
∵点C(3,0),D(0,﹣1),E(1,﹣4),
∴CO=DF=3,DO=EF=1,
根据勾股定理,CD=![]() ,
,
在△COD和△DFE中,
∵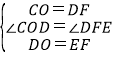 ,
,
∴△COD≌△DFE(SAS),
∴∠EDF=∠DCO,
又∵∠DCO+∠CDO=90°,
∴∠EDF+∠CDO=90°,
∴∠CDE=180°﹣90°=90°,
∴CD⊥DE,
①分OC与CD是对应边时,
∵△DOC∽△PDC,
∴![]() ,
,
即![]() ,
,
解得DP=![]() ,
,
过点P作PG⊥y轴于点G,
则 ![]() ,
,
即![]() ,
,
解得DG=1,PG=![]() ,
,
OG=DO+DG=1+1=2,
所以,点P(![]() ,﹣2);
,﹣2);
②OC与DP是对应边时,
∵△DOC∽△CDP,
∴![]() ,
,
即 ![]() ,
,
解得DP=3![]() ,
,
过点P作PG⊥y轴于点G,
则![]() ,
,
即 ![]() ,
,
解得DG=9,PG=3,
OG=OD+DG=1+9=10,
所以,点P的坐标是(3,﹣10),
综上所述,满足条件的点P共有2个,其坐标分别为(![]() ,﹣2)、(3,﹣10).
,﹣2)、(3,﹣10).