题目内容
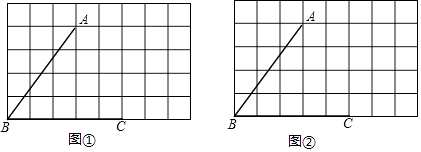
【题目】如图，在△ABC中，∠BAC=90°，AB=AC=2，以AB为直径的圆交BC于D，则图中阴影部分的面积为（ ）
A.1
B.2
C.1+ 
D.2﹣
【答案】A
【解析】解：连接AD，OD
∵∠BAC=90°，AB=AC=2
∴△ABC是等腰直角三角形
∵AB是圆的直径
∴∠ADB=90°
∴AD⊥BC
∴点D是BC的中点
∴OD是△ABC的中位线
∴∠DOA=90°
∴△ODA，△ADC都是等腰直角三角形
∴两个弓形的面积相等
∴阴影部分的面积=S△ADC= 
AD2=1．
所以答案是：A．
【考点精析】利用等腰直角三角形和三角形中位线定理对题目进行判断即可得到答案，需要熟知等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．
阅读快车系列答案
【题目】某校对七、八、九年级的学生进行体育水平测试，成绩评定为优秀、良好、合格、不合格四个等第．为了解这次测试情况，学校从三个年级随机抽取200名学生的体育成绩进行统计分析．相关数据的统计图、表如下：
各年级学生成绩统计表 | ||||
优秀 | 良好 | 合格 | 不合格 | |
七年级 | a | 20 | 24 | 8 |
八年级 | 29 | 13 | 13 | 5 |
九年级 | 24 | b | 14 | 7 |
根据以上信息解决下列问题：
（1）在统计表中，a的值为 ， b的值为；
（2）在扇形统计图中，八年级所对应的扇形圆心角为度；
（3）若该校三个年级共有2000名学生参加考试，试估计该校学生体育成绩不合格的人数．
【题目】某村为了尽早摆脱贫穷落后的现状，积极响应国家号召，15位村民集资8万元，承包了一些土地种植有机蔬菜和水果，种这两种作物每公顷需要人数和投入资金如下表：
作物种类 | 每公顷所需人数/人 | 每公顷投入资金/万元 |
蔬菜 | 4 | 2 |
水果 | 5 | 3 |
在现有条件下，这15位村民应承包多少公顷土地，怎样安排能使每人都有事可做，并且资金正好够用？
