题目内容
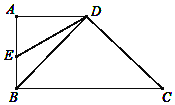
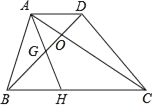
【题目】如图,梯形ABCD的对角线AC、BD相交于O,点H为BC上一点,连接AH交BD于点G.若AD=3,BC=9,BH:HC=1:2,则GO:BG=( )
A.1:2B.1:3C.2:3D.11:20
【答案】A
【解析】
连接DH,则四边形ABHD为平行四边形,根据平行四边形的性质可得出BG=![]() BD,由AD∥BC可得出△AOD∽△COB,根据相似三角形的性质可求出OD=
BD,由AD∥BC可得出△AOD∽△COB,根据相似三角形的性质可求出OD=![]() BD,由GO=BD-BG-OD可得出GO=
BD,由GO=BD-BG-OD可得出GO=![]() BD,将其代入GO:BG中即可得出结论.
BD,将其代入GO:BG中即可得出结论.
解:连接DH,如图所示.
∵BC=9,BH:HC=1:2,
∴BH=3=AD.
又∵四边形ABCD为梯形,
∴AD∥BC,
∴四边形ABHD为平行四边形,
∴BG=![]() BD.
BD.
∵AD∥BC,
∴△AOD∽△COB,
∴![]() ,
,
∴OD=![]() BD=
BD=![]() BD,
BD,
∴GO=BD﹣BG﹣OD=![]() BD,
BD,
∴GO:BG=1:2.
故选:A.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目