题目内容
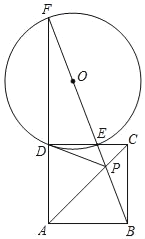
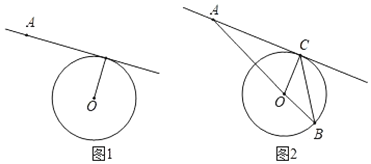
【题目】如图1,点A是⊙O外一点.
(1)过点A作⊙O的切线(要求:尺规作图,保留作图痕迹,不写作法);
(2)如图2,设AC是⊙O的切线,点C是切点,已知tan∠A=![]() ,求tan∠ABC的值.
,求tan∠ABC的值.
【答案】(1)见解析;(2)![]()
【解析】
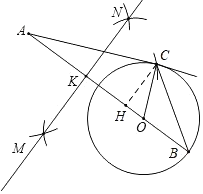
(1)如图,作线段AO的垂直平分线MN交AO于K,以K为圆心,OK为半径画弧交⊙O于点C,连接AC,OC,直线AC即为所求;
(2)作CH⊥OA于H.证明∠A=∠OCH,推出tan∠A=tan∠OCH=![]() ,设OH=a,CH=2a,则OC=OB=
,设OH=a,CH=2a,则OC=OB=![]() a,在Rt△BCH中,根据tan∠ABC=
a,在Rt△BCH中,根据tan∠ABC=![]() 求解即可.
求解即可.
解:(1)如图,如图,作线段AO的垂直平分线MN交AO于K,以K为圆心,OA为半径画弧交⊙O于点C,连接AC,OC,直线AC即为所求.
(2)作CH⊥OA于H.
∵AC是⊙O的切线,
∴AC⊥OC,
∴∠ACO=∠CHO=90°,
∵∠A+∠AOC=90°,∠OCH+∠AOC=90°,
∴∠A=∠OCH,
∴tan∠A=tan∠OCH=![]() =
=![]() ,设OH=a,CH=2a,则OC=OB=
,设OH=a,CH=2a,则OC=OB=![]() a,
a,
在Rt△BCH中,tan∠ABC=![]() .
.

 通城学典默写能手系列答案
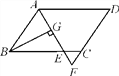
通城学典默写能手系列答案【题目】如图,梯形ABCD的对角线AC、BD相交于O,点H为BC上一点,连接AH交BD于点G.若AD=3,BC=9,BH:HC=1:2,则GO:BG=( )
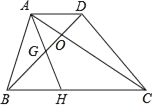
A.1:2B.1:3C.2:3D.11:20
【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.