题目内容

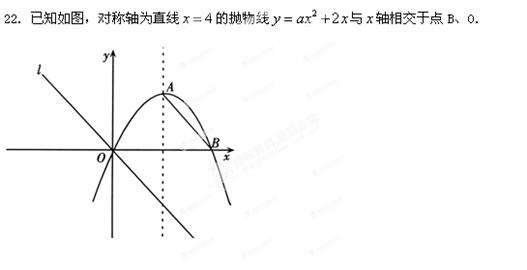 (1）求抛物线的解析式，并求出顶点A的坐标.

(2) 连结AB，平移AB所在的直线，使其经过原点O，得到直线.点是上一动点,当△的周长最小时，求点P的坐标.

（3）当△的周长最小时，在直线AB的上方是否存在一点Q，使以A，B，Q为顶点的三角形与△POB相似，若存在，直接写出点Q的坐标；若不存在，说明理由.（规定：点Q的对应顶点不为点O）

 

（1），（4，4）(2) （2，-2）(3)存在，点坐标为（8，16）、（20，4）（8,2）、（6,4） 

【解析】（1）∵点B与O（0，0）关于直线x=4对称,

∴点B坐标为（8，0）.

将点B坐标代入得：

64+16=0,

∴=.

∴抛物线解析式为.               2分

当=4时，,

∴顶点A坐标为（4，4）.                  2分

（说明：可用对称轴为,求值,用顶点式求顶点A坐标.）

（2）设直线AB解析式为y=kx+b.

∵A(4,4),B(8,0),

∴ 解得,   ∴.-

∵直线∥AB且过点O,

∴直线解析式为.

A关于直线的对称点是A1（-4，-4），连接A1B，则直线A1B的函数关系式是

由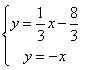  得交点P（2，-2）                         4分

 (3)存在，点坐标为（8，16）、（20，4）（8,2）、（6,4）         4分

主要考查了一次函数、二次函数解析式的确定，函数图象交点及图形面积的求法等重要知识点，同时还考查了分类讨论的数学思想，难度较大

 

练习册系列答案
相关题目
在平面直角坐标系xOy中，抛物线y=-
12
x2+bx+c与x轴交于A、B两点（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，且OA=2，OC=3．
（1）求抛物线的解析式；
（2）若点E在第一象限内的此抛物线上，且OE⊥BC于D，求点E的坐标；
（3）在抛物线的对称轴上是否存在一点P，使线段PA与PE之差的值最大？若存在，请求出这个最大值和点P的坐标；若不存在，请说明理由．
（2013•江都市二模）如图，在直角坐标系中，抛物线y=ax2+2x+c过点A（-1，0）、B（3，0）且与y轴交与点C，点D为抛物线对称轴x=l上一动点．
（1）求抛物线的解析式；
（2）求当AD+CD最小时点D的坐标；
（3）有这样的点D能使△ACD为直角三角形吗？若能，求出点D的坐标；若不能请说明理由．
已知抛物线y=ax2-2x+c与x轴交于A（-1，0）、B两点，与y轴交于点C，对称轴为x=1，顶点为E，直线y=-
13
x+1交y轴于点D．
（1）求抛物线的解析式；
（2）求证：△BCE∽△BOD；
（3）点P是抛物线上的一个动点，当点P运动到什么位置时，△BDP的面积等于△BOE的面积？
（2013•黔东南州）已知抛物线y1=ax2+bx+c（a≠0）的顶点坐标是（1，4），它与直线y2=x+1的一个交点的横坐标为2．
（1）求抛物线的解析式；
（2）在给出的坐标系中画出抛物线y1=ax2+bx+c（a≠0）及直线y2=x+1的图象，并根据图象，直接写出使得y1≥y2的x的取值范围；
（3）设抛物线与x轴的右边交点为A，过点A作x轴的垂线，交直线y2=x+1于点B，点P在抛物线上，当S△PAB≤6时，求点P的横坐标x的取值范围．
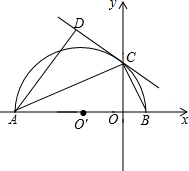如图，在平面直角坐标系xOy中，AB在x轴上，以AB为直径的半⊙O′与y轴正半轴交于点C，连接BC，AC．CD是半⊙O′的切线，AD⊥CD于点D．
（1）求证：∠CAD=∠CAB；
（2）已知抛物线y=ax2+bx+c过A、B、C三点，AB=10，tan∠CAD=
12
．
①求抛物线的解析式；
②判断抛物线的顶点E是否在直线CD上，并说明理由；
③在抛物线上是否存在一点P，使四边形PBCA是直角梯形？若存在，直接写出点P的坐标（不写求解过程）；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网