题目内容
已知五个数据中的一个数是15,另外的四个数的平均数为14,那么这五个数的和为________.
71
分析:根据另外的四个数的平均数为14,即可得出这4个数的和,进而得出这五个数的和.
解答:∵五个数据中的一个数是15,另外的四个数的平均数为14,
∴这五个数的和为:15+4×14=71.
故答案为:71.
点评:本题考查了平均数的定义.平均数等于所有数据的和除以数据的个数.
分析:根据另外的四个数的平均数为14,即可得出这4个数的和,进而得出这五个数的和.
解答:∵五个数据中的一个数是15,另外的四个数的平均数为14,
∴这五个数的和为:15+4×14=71.
故答案为:71.
点评:本题考查了平均数的定义.平均数等于所有数据的和除以数据的个数.

练习册系列答案
相关题目
2012年3月25日浙江省环境厅第一次发布七城市PM2.5浓度数据(表一)
2012年3月24日PM2.5监测试报数据
| 城市名称 | 日平均浓度(微克/立方米) | 分指数(IAOI) |
| 杭州 | 35 | 50 |
| 宁波 | 49 | |
| 温州 | 33 | 48 |
| 湖州 | 40 | 57 |
| 嘉兴 | 33 | 48 |
| 绍兴 | 44 | |
| 舟山 | 30 | 43 |
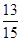 ,绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10,求绍兴和宁波两市的分指数;
,绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10,求绍兴和宁波两市的分指数;(2)问上述七城市中分指数的极差是多少?位于中位数的城市是哪一个城市?
(3)描述一组数据的离散程度,我们可以用“极差”、“方差”、“平均差”[平均差公式为
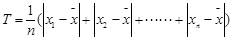 ,求杭州,温州,湖州,嘉兴,舟山五个城市中分指数的平均差。
,求杭州,温州,湖州,嘉兴,舟山五个城市中分指数的平均差。 2012年3月25日浙江省环境厅第一次发布七城市PM2.5浓度数据(表一)
2012年3月24日PM2.5监测试报数据
|
城市名称 |
日平均浓度(微克/立方米) |
分指数(IAOI) |
|
杭州 |
35 |
50 |
|
宁波 |
49 |
|
|
温州 |
33 |
48 |
|
湖州 |
40 |
57 |
|
嘉兴 |
33 |
48 |
|
绍兴 |
44 |
|
|
舟山 |
30 |
43 |
(1)已知绍兴和宁波两市的分指数的和是杭州、湖州、舟山三市分指数和的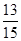 ,绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10,求绍兴和宁波两市的分指数;
,绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10,求绍兴和宁波两市的分指数;
(2)问上述七城市中分指数的极差是多少?位于中位数的城市是哪一个城市?
(3)描述一组数据的离散程度,我们可以用“极差”、“方差”、“平均差”[平均差公式为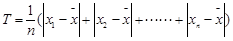 ,求杭州,温州,湖州,嘉兴,舟山五个城市中分指数的平均差。
,求杭州,温州,湖州,嘉兴,舟山五个城市中分指数的平均差。
2012年3月25日浙江省环境厅第一次发布七城市PM2.5浓度数据(表一)
2012年3月24日PM2.5监测试报数据
| 城市名称 | 日平均浓度(微克/立方米) | 分指数(IAOI) |
| 杭州 | 35 | 50 |
| 宁波 | 49 | ▲ |
| 温州 | 33 | 48 |
| 湖州 | 40 | 57 |
| 嘉兴 | 33 | 48 |
| 绍兴 | 44 | ▲ |
| 舟山 | 30 | 43 |
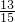 ,绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10,求绍兴和宁波两市的分指数;
,绍兴分指数的5倍与宁波分指数的3倍的差比温州和嘉兴两市分指数的和大10,求绍兴和宁波两市的分指数;(2)问上述七城市中分指数的极差是多少?位于中位数的城市是哪一个城市?
(3)描述一组数据的离散程度,我们可以用“极差”、“方差”、“平均差”[平均差公式为T=
 (|x1
(|x1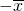 |+|x2-
|+|x2- |+…+|xn
|+…+|xn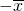 |),求杭州,温州,湖州,嘉兴,舟山五个城市中分指数的平均差.
|),求杭州,温州,湖州,嘉兴,舟山五个城市中分指数的平均差.