题目内容
【题目】如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为 时,由点A、C、D组成的三角形与△AOB相似.
【答案】D点坐标为(3,0)或(﹣![]() ,0).
,0).
【解析】
试题分析:先根据勾股定理求出AB的长,进而可得出AC的长,再根据△AOB∽△ADC与△AOB∽△ACD两种情况进行讨论.
解:∵在直角形坐标系中有两点A(6,0)、B(0,8),
∴OA=6,OB=8,
∴AB=![]() =10.
=10.
∵点C为AB的中点,
∴AC=5.
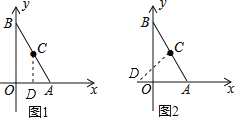
当△AOB∽△ADC时,
![]() =
=![]() ,即
,即![]() =
=![]() ,解得AD=3,
,解得AD=3,
∴OD=OA﹣AD=6﹣3=3,
∴D(3,0);
当△AOB∽△ACD时,
![]() =
=![]() ,即
,即![]() =
=![]() ,解得AD=
,解得AD=![]() ,
,
∵AD﹣OA=![]() ﹣6=
﹣6=![]() ,
,
∴D(﹣![]() ,0).
,0).
综上所述,D点坐标为(3,0)或(﹣![]() ,0).
,0).

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目


