题目内容
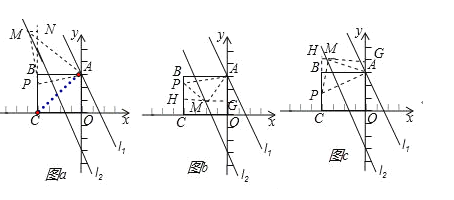
【题目】如图，在矩形ABCO中，点O为坐标原点，点B的坐标为（﹣4，3），点A，C在坐标轴上，将直线l1：y＝﹣2x+3向下平移6个单位长度得到直线l2．
（1）求直线l2的解析式；
（2）求直线l2与两坐标轴围成的三角形的面积S；
（3）已知点M在第二象限，且是直线l2上的点，点P在BC边上，若△APM是等腰直角三角形，求点M的坐标．
【答案】（1）y＝﹣2x﹣3；（2）
；（3）点M的坐标为（﹣
，
）或（﹣2，1）或（﹣
，
）．
【解析】
（1）根据平移规律得出直线l2的解析式即可；
（2）根据坐标轴上点的坐标特征可求直线l1与x轴，直线l2与AB的交点坐标；
（3）分三种情况：①若点A为直角顶点时，点M在第二象限；若点P为直角顶点时，点M在第二象限；③若点M为直角顶点时，点M在第二象限；进行讨论可求点M的坐标；
解：（1）直线l2的解析式为y＝﹣2x+3﹣6＝﹣2x﹣3．
（2）由（1）知直线l2的解析式为y＝﹣2x﹣3，令y＝0，即﹣2x﹣3＝0，
∴x＝﹣
；
令x＝0，则y＝﹣3，
∴S＝
×3×＝．
（3）若△APM是等腰直角三角形，分以下三种情况讨论：①当点A为直角顶点时，∠MPA＝45°，连接AC，如图a.
∵点M在第二象限，若∠MAP＝90°，则点M必在AB上方，
∴∠MPA＞∠BPA＞∠BCA＝45°，这与∠MPA＝45°矛盾，
∴点M不存在；
②当点P为直角顶点时，即∠MPA＝90°．
∵M在第二象限，
∴点M必在AB上方，如图a，过点M作MN⊥CB交CB的延长线于点N，易证△ABP≌△PNM，
∴PN＝AB＝4，MN＝BP．
∵B（﹣4，3），
∴CB＝3．设点M的坐标为（x，﹣2x﹣3），则BP＝MN＝﹣4﹣x，CN＝﹣2x﹣3．
∵CN＝CB+PN﹣BP，
∴﹣2x﹣3＝3+4﹣（﹣4﹣x），
∴x＝﹣，则﹣2x﹣3＝，
∴点M的坐标为（﹣，）；
③当点M为直角顶点时，分两种情况讨论：如图b，当点M在AB下方时，过点M作HG⊥OA交OA于点G，交BC于点H，易证△MPH≌△AMG，
∴MH＝AG．设点M的坐标为（a，﹣2a﹣3），则AG＝3﹣（﹣2a﹣3）＝6+2a，MG＝﹣a，
∴HG＝MH+MG＝AG+MG＝6+2a﹣a＝4，
∴a＝﹣2，则﹣2a﹣3＝1．
∴点M的坐标为（﹣2，1）；
如图c，当点M在AB上方时，同理可得﹣2a﹣6﹣a＝4，
∴a＝﹣，则﹣2a﹣3＝，
∴点M2的坐标为（﹣，），
综上所述，点M的坐标为（﹣，）或（﹣2，1）或（﹣，）．
