题目内容
若正方形ABCD的边长为4,点E、F在正方形ABCD的边上,但不与正方形ABCD的顶点重合,且∠AEF=90°,AF=5,求BE的长.
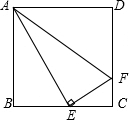 解:∵正方形ABCD的边长为4,AF=5,
解:∵正方形ABCD的边长为4,AF=5,∴由勾股定理得:DF=3,
∴CF=1,
∵∠BAE和∠EFC都是∠AEB的余角.
∴∠BAE=∠FEC.
∴△ABE∽△ECF
那么AB:EC=BE:CF,
∵AB=4,BE=x,EC=4-x,CF=1.
∴AB•CF=EC•BE,
即4×1=(4-x)x.
解得x=2.
∴BE的长为2.
分析:在直角三角形ADF中,利用勾股定理求得DF的长,进而求得FC的长,设BE=x,利用△ABE∽△ECF得到比例式后即可求得x的值.
点评:本题综合考查了正方形和相似三角形的性质.根据条件得出相似三角形,用未知数表示出相关线段是解题的关键.

练习册系列答案
相关题目
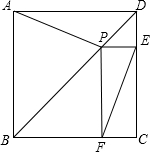 如图,点P是正方形ABCD对角线BD上一点,作PE⊥DC于E,PF⊥BC于F.
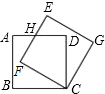
如图,点P是正方形ABCD对角线BD上一点,作PE⊥DC于E,PF⊥BC于F. (2012•眉山)已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF.
(2012•眉山)已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF. 如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE
如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE