题目内容
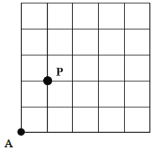
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.例如从A到B记为:A →B(+1,+3),从B到A记为:B→A(﹣1,-3),其中第一个数表示左右方向,第二个数表示上下方向.


(1)图中A →C(______,______),B →C(______,______),C→_______(+1,﹣2);
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)从A处去P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
【答案】(1)(+3,+4),(+2,+1),D(2)10(3)图见解析(4)(-2,-2)
【解析】
(1)根据题干中“向上向右走为正,向下向左走为负,第一个数表示左右方向,第二个数表示上下方向”判断出起点到终点的移动方法和距离即可.
(2)分别计算出A到B,B到C,C到D运动的路程,再求和.
(3)按照“第一个数的正与负表示右与左移,第二个数的正与负表示上与下移动”这个规律,进行判断.可以先看左右方向表示的数字和即为左右方向移动的距离,再看上下方向表示的数字和即为上下移动的距离..
(4)把M点看作坐标原点,则A与N的坐标就分别为(3-a,b-4),(5-a,b-2),再通过坐标差值的正负来判断位置.
(1) A →C:先向右移动3个单位,再向上移动4个单位,则为(+3,+4)
B →C:先向右移动2个单位,再向上移动1个单位,则为(+2,+1)
(+1,﹣2)表示为C点向右移动1个单位,向下移动2个单位,则为C→D.
(2) A →B的路程为:1+3=4,B →C的路程为:2+1=3,C→D的路程为1+2=3
所以A→B→C→D走过的路程为4+3+3=10.
(3)左右方向的数字和为:(+2)+(+2)+(-2)+(-1)=+1,即代表向右移动了1个单位.
上下方向的数字和为:(+2)+(-1)+(+3)+(-2)=+2,即代表向上移动了2个单位.
所以,从A处去P处向右移动了2个单位,向上移动了2个单位.位置如图所示:
(4) 由M→A(3-a,b-4),M→N(5-a,b-2)可知,此时可以把M点看作坐标原点,则A点的坐标为(3-a,b-4),N点的坐标为(5-a,b-2),则N→A,左右方向,![]() ,所以A在N的左侧2个单位处.上下方向,
,所以A在N的左侧2个单位处.上下方向,![]() ,所以A在N的下方2个单位处.所以,N→A记作(-2,-2)
,所以A在N的下方2个单位处.所以,N→A记作(-2,-2)
故答案为:(1)(+3,+4),(+2,+1),D(2)10(3)图见解析(4)(-2,-2)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案