题目内容
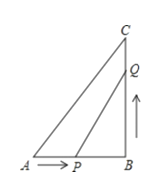
【题目】如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，动点P从点A开始沿AB边向B以1cm/s的速度移动（不与点B重合）；动点Q从B点开始沿BC边向点C以2cm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，出发多少秒后，四边形APQC的面积为16cm2？
【答案】2
【解析】
根据题意表示出四边形APQC的面积，进而得出方程求出答案．
解：设t秒后，四边形APQC的面积为16cm2，
由题意得：S△ABC=
×6×8=24（cm2），BP=6-t，BQ=2t，
∴24-2t（6-t）=16，
解得：t1=2，t2=4，
当t=4时，BQ=2×4=8，
∵Q不与点C重合，
∴t=4不合题意舍去，
所以2秒后，四边形APQC的面积为16cm2．
练习册系列答案
口算题天天练系列答案
相关题目
【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式.（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
【题目】用棋子摆成的“
”字形图，如图所示：
……
(1)填写下表：
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 |
|
| ______ | _____ | … | ______ |
(2)写出第
个“”字形图案中棋子的个数(用含的代数式表示)：
(3)第20个“”字形图案共有棋子多少个？
