题目内容
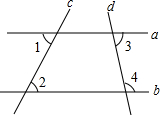
如图,已知AB∥CD∥EF,且∠A=50°,∠F=120°,DG平分∠ADF,求∠CDG的度数.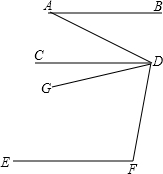
解:∵AB∥CD
∴∠A=∠ADC______
又∵∠A=50°
∴∠______=50°
∵CD∥EF
∴∠F+∠______=180°(两直线平行,同旁内角互补)
又∵∠F=120°
∴∠CDF=______
∴∠ADF=______
∵DG平分∠ADF
∴∠ADG=
∠______=______°______
∴∠CDG=∠ADG-∠______=______°.

解:∵AB∥CD
∴∠A=∠ADC______
又∵∠A=50°
∴∠______=50°
∵CD∥EF
∴∠F+∠______=180°(两直线平行,同旁内角互补)
又∵∠F=120°
∴∠CDF=______
∴∠ADF=______
∵DG平分∠ADF
∴∠ADG=
| 1 |
| 2 |
∴∠CDG=∠ADG-∠______=______°.
∵AB∥CD,
∴∠A=∠ADC,(两直线平行,内错角相等)
又∵∠A=50°,
∴∠ADC=50°,
∵CD∥EF,
∴∠F+∠CDF=180°(两直线平行,同旁内角互补 ),
又∵∠F=120°,
∴∠CDF=60°,
∴∠ADF=∠ADC+∠CDF=110°,
∵DG平分∠ADF
∴∠ADG=
∠ADF=55°(角平分线的定义),
∴∠CDG=∠ADG-∠ADC=5°.
故答案为:两直线平行,内错角相等;ADC;CDF;60°;110°;ADF;55;角平分线的定义;ADC;5.

∴∠A=∠ADC,(两直线平行,内错角相等)
又∵∠A=50°,
∴∠ADC=50°,
∵CD∥EF,
∴∠F+∠CDF=180°(两直线平行,同旁内角互补 ),
又∵∠F=120°,
∴∠CDF=60°,
∴∠ADF=∠ADC+∠CDF=110°,
∵DG平分∠ADF
∴∠ADG=
| 1 |
| 2 |
∴∠CDG=∠ADG-∠ADC=5°.
故答案为:两直线平行,内错角相等;ADC;CDF;60°;110°;ADF;55;角平分线的定义;ADC;5.


练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目