题目内容
【题目】阅读下面材料：
小天在学习锐角三角函数中遇到这样一个问题：在Rt△ABC中，∠C=90°，∠B=22.5°，则tan22.5°=
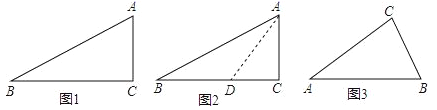
小天根据学习几何的经验，先画出了几何图形（如图1），他发现22.5°不是特殊角，但它是特殊角45°的一半，若构造有特殊角的直角三角形，则可能解决这个问题．于是小天尝试着在CB边上截取CD=CA，连接AD（如图2），通过构造有特殊角（45°）的直角三角形，经过推理和计算使问题得到解决．
请回答：tan22.5°= ．
参考小天思考问题的方法，解决问题：
如图3，在等腰△ABC 中，AB=AC，∠A=30°，请借助△ABC，构造出15°的角，并求出该角的正切值．
【答案】（1）
﹣1；﹣1；（2）2﹣
．
【解析】
试题分析：如图2，设CD=CA=a，△ACD为等腰直角三角形，则AD=a，易得∠DAB=∠B=22.5°，所以DB=DA=a，再在Rt△ABC中，利用正切定义可计算出tanB=﹣1，即tan22.5°=﹣1；
如图3，延长BA到D，使AD=AB，则AB=AD=AC，则∠D=∠ACD，利用三角形外角性质易得∠D=15°，作CH⊥AB于H，设CH=x，利用含30度三边的关系得到AC=2x，AH=x，则AD=AC=2x，DH=AD+AH=（2+）x，然后在Rt△DCH中，利用正切的定义可计算出tanD=2﹣，即tan15°=2﹣．
试题解析：如图2，设CD=CA=a，则AD=a，
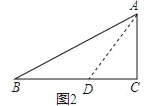
∵∠B=22.5°，∠ADC=45°，
∴∠DAB=22.5°，
∴∠DAB=∠B，
∴DB=DA=a，
∴BC=BD+CD=（+1）a，
在Rt△ABC中，tanB=
，
即tan22.5°=﹣1；
如图3，延长BA到D，使AD=AB，则AB=AD=AC，
∴∠D=∠ACD，
∵∠CAB=∠D+∠ACD=30°，
∴∠D=15°，
作CH⊥AB于H，设CH=x，则AC=2x，AH=x，
∴AD=AC=2x，
∴DH=AD+AH=（2+）x，
在Rt△DCH中，tanD=
，
即tan15°=2﹣．
