题目内容
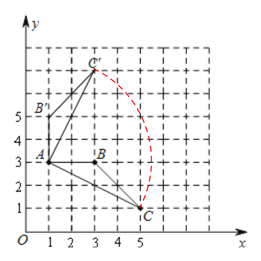
【题目】如图：（1）写出△ABC中点A、点C坐标；（2）画出△ABC绕点A管好逆时针旋转90°后的△AB＇C＇；（3）在（2）的条件下，求点C旋转到C＇所经过的路线长。（结果保留
）
【答案】（1）A（1，3） C（5，1）；（2）见解析；（3）
.
【解析】试题分析：
（1）观察图中所建立的坐标系即可得到点A、C的坐标；
（2）分别描出点B、C绕点A逆时针旋转90°后所得对应点B′、C′，再顺次连接A、B′、C′三点即可得到所求三角形；
（3）如图，由（2）可知，点C的运动路线是
，其对应的圆心角为90°，半径为AC=
，这样由弧长公式计算出
的长度即可.
试题解析：
由图可知：（1）点A的坐标为：（1，3）、 点C的坐标为：（5，1）；
（2）如图所示：△AB′C′为所求三角形；
（3）如上图， 
的长度为点C旋转到点C′所经过的路线长，
由题意可知：AC=
，∠CAC′=90°，
∴
，即点C旋转到C＇所经过的路线长为
.
练习册系列答案
相关题目
