题目内容
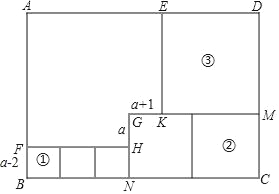
【题目】如图所示,用三种大小不等的正方形①②③和…个缺角的正方形拼成一个长方形ABCD(不重叠且没有缝隙),若GH=a,GK=a+1,BF=a﹣2
(1)试用含a的代数式表示:正方形②的边长CM的长= ,正方形③的边长DM的长= ;
(2)求长方形ABCD的周长(用含a的代数式表示);并求出当a=3时,长方形周长的值.
【答案】(1)2a﹣2,3a﹣5;(2)56.
【解析】
(1)根据正方形的性质和线段的和差关系即可得出CM和DM;
(2)先求出长方形ABCD的长和宽,再用2(长+宽)即可得出长方形ABCD的面积,将a=3代入即可求得周长.
(1)CM=BF+GH=a﹣2+a=2a﹣2,
DM=MK=2CM﹣GK=2(2a﹣2)﹣(a+1)=3a﹣5,
故答案为:2a﹣2,3a﹣5;
(2)长方形ABCD的宽DC为:DM+CM=5a﹣7,
长AD为:BN+NC=DM+a+1+3(a﹣2)=3a﹣5+a+1+3a﹣6=7a﹣10,
周长为:2(AD+DC)=2(5a﹣7)+2(7a﹣1)=24a﹣16,
当a=3时,周长为:24×3﹣16=56.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目