Question

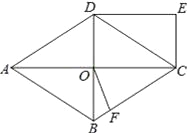
【题目】（6分）如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．

（1）求证：四边形OCED为矩形；

（2）过点O作OF⊥BC，垂足为F，若AC=16，BD=12，则OF=　　．

Answer 1

【答案】（1）见解析；（2）4.8

【解析】试题分析：（1）先证明四边形OCED是平行四边形，再由菱形的性质得出对角线互相垂直，得出∠COD=90°，即可得出结论；

（2）由菱形的性质求出OC=AC=8，OB=BD=6，由勾股定理求出BC，再由△BOC面积的计算方法求出OF即可．

（1）证明：∵DE∥AC，CE∥BD，

∴四边形OCED是平行四边形，

∵四边形ABCD是菱形，

∴AC⊥BD，

∴∠COD=90°，

∴四边形OCED为矩形；

（2）解：∵四边形ABCD是菱形，

∴AC⊥BD，OC=AC=8，OB=BD=6，

由勾股定理得：BC==10，

∵△BOC的面积=BCOF=OBOC，

∴OF==4.8．

故答案为：4.8．