��Ŀ����
����Ŀ���������о�����תͼ���ж�Ӧ�߶�����ֱ�ߵļнǣ�С�ڵ���![]() �Ľǣ�����ת�ǵĹ�ϵ��
�Ľǣ�����ת�ǵĹ�ϵ��
�������̽���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת���߶�
˳ʱ����ת���߶�![]() �����е�
�����е�![]() ���
���![]() ��Ӧ����
��Ӧ����![]() ���
���![]() ��Ӧ����ת�ǵĶ���Ϊ
��Ӧ����ת�ǵĶ���Ϊ![]() ����
����![]() ��
��
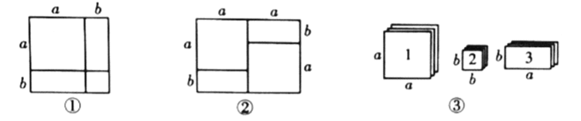
��1����ͼ��1����![]() ʱ���߶�
ʱ���߶�![]() ��
��![]() ����ֱ�н�Ϊ______��
����ֱ�н�Ϊ______��
��2����ͼ��2����![]() ʱ���߶�
ʱ���߶�![]() ��
��![]() ����ֱ�н�Ϊ_____��
����ֱ�н�Ϊ_____��
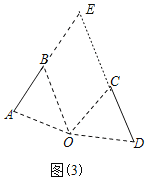
��3����ͼ��3������![]() ʱ��ֱ��
ʱ��ֱ��![]() ��ֱ��
��ֱ��![]() �н�����ת��
�н�����ת��![]() ������������������ϵ����˵�����ɣ�
������������������ϵ����˵�����ɣ�
���γɽ��ۣ���תͼ���У�����ת��С��ƽ��ʱ����Ӧ�߶�����ֱ�ߵļн�����ת��_____��
�������ع㣩�������γɵĽ��������������⣺
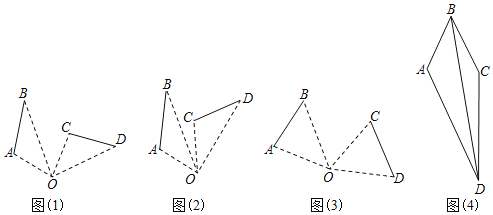
��4����ͼ��4�����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() �ij��ȣ�
�ij��ȣ�
���𰸡���1��90������2��60������3�����������ɼ���������Ȼ�����4��![]() .
.
��������
��1��ͨ������������ͼ1���ӳ�DC��AB��F����BO��E������ͨ����ת���ʵõ�AB=CD��OA=OC��BO=DO��֤����AOB�ա�COD��������á�B=��D�á�BFE=��EOD=90��
��2��ͨ������������ͼ2���ӳ�DC��AB��F����BO��E��ͬ��1���á�BFE=��EOD=60��
��3��ͨ������������ͼ3��ֱ��![]() ��ֱ��
��ֱ��![]() ���е��������ת��
���е��������ת��![]() ������ �ӳ�
������ �ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ͨ��֤��
ͨ��֤��![]() ��
��![]() ����ͨ��ƽ�ǵĶ�����ı����ڽǺͶ�����֤��
����ͨ��ƽ�ǵĶ�����ı����ڽǺͶ�����֤��![]() ��
��
�γɽ��ۣ�ͨ�����⣨1����2����3�������ܽ����תͼ���У�����ת��С��ƽ��ʱ����Ӧ�߶�����ֱ�ߵļн�����ת����Ȼ���
��4��ͨ������������ͼ����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת��ʹ��
˳ʱ����ת��ʹ��![]() ��
��![]() �غϣ��õ�
�غϣ��õ�![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ���ɵ�
���ɵ�![]() ����һ���õ���BDF�ǵȱ������Σ�
����һ���õ���BDF�ǵȱ������Σ�![]() �������ù��ɶ������
�������ù��ɶ������![]() .
.
��1���⣺��1����ͼ1���ӳ�DC��AB��F����BO��E��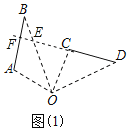
����=90��
���BOD=90��
���߶�AB�Ƶ�O˳ʱ����ת���߶�CD��
��AB=CD��OA=OC��BO=DO
���AOB�ա�COD��SSS��
���B=��D
�ߡ�B=��D����OED=��BEF
���BFE=��EOD=90��
�ʴ�Ϊ��90��
��2����ͼ2���ӳ�DC��AB��F����BO��E��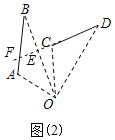
����=60��
���BOD=60��
���߶�AB�Ƶ�O˳ʱ����ת���߶�CD��
��AB=CD��OA=OC��BO=DO
���AOB�ա�COD��SSS��
���B=��D
�ߡ�B=��D����OED=��BEF
���BFE=��EOD=60��
�ʴ�Ϊ��60��
��3��ֱ��![]() ��ֱ��
��ֱ��![]() ���е��������ת��
���е��������ת��![]() ������
������
�ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]()
���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת���߶�
˳ʱ����ת���߶�![]() ��
��
��![]() ��
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��ֱ��![]() ��ֱ��
��ֱ��![]() ���е��������ת��
���е��������ת��![]() ������
������
�γɽ��ۣ���תͼ���У�����ת��С��ƽ��ʱ����Ӧ�߶�����ֱ�ߵļн�����ת����Ȼ���
��4����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת��ʹ��
˳ʱ����ת��ʹ��![]() ��
��![]() �غϣ��õ�
�غϣ��õ�![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��

����ת��Ϊ![]() ��
��![]()
��![]() ��
��![]() ��
��![]() ��
��
���BDF�ǵȱ������Σ�
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�