题目内容
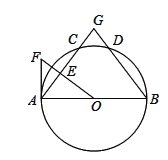
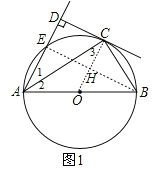
【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3![]() ,求DE的长;
,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3![]() ,求图中阴影部分面积.
,求图中阴影部分面积.

【答案】(1)证明见解析;(2)3;(3)![]()
【解析】
(1)连接OC,如图1,先证明∠1=∠3得到OC∥AD,再利用平行线的性质得OC⊥CD,然后根据切线的判定定理得到结论;
(2)连接BE交OC于H,如图1,利用圆周角定理得∠AEB=90°,易得四边形CDEH为矩形,则CD=EH=3![]() ,CH=ED,利用垂径定理得BH=3
,CH=ED,利用垂径定理得BH=3![]() ,然后利用勾股定理计算出OH后计算出CH,从而得到DE的长;
,然后利用勾股定理计算出OH后计算出CH,从而得到DE的长;
(3)连接OC,如图2,设⊙O的半径为r,利用角平分线的性质得CD=CF,则根据勾股定理得AD=AF,于是可计算出OF=1.5,再证明△ACF∽△ABC,利用相似比得到![]() ,解得r=3,接着在Rt△OCF中利用解直角三角形得到∠COF=60°,CF=
,解得r=3,接着在Rt△OCF中利用解直角三角形得到∠COF=60°,CF=![]() ,然后根据扇形面积公式,利用图中阴影部分面积=S扇形BOC-S△OCB进行计算.
,然后根据扇形面积公式,利用图中阴影部分面积=S扇形BOC-S△OCB进行计算.
(1)连接OC,如图1,
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴DC是⊙O切线;
(2)连接BE交OC于H,如图1,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵OC∥AD,
∴∠OHB=90°,
∴EH=BH,四边形CDEH为矩形,
∴CD=EH=3![]() ,CH=ED,
,CH=ED,
∴BH=3![]() ,
,
在Rt△OBH中,OH=![]() =3,
=3,
∴CH=6-3=3,
∴DE=3;
(3)连接OC,如图2,设⊙O的半径为r,
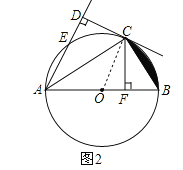
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CD=CF,
∴AD=AF=AO+OF,
∵AD-OA=1.5,
∴AO+OF-OA=1.5,即OF=1.5,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAF=∠BAC,
∴△ACF∽△ABC,
∴![]() ,即
,即![]() ,
,
解得r=-![]() (舍去)或r=3,
(舍去)或r=3,
在Rt△OCF中,cos∠COF=![]() ,
,
∴∠COF=60°,
∴CF=![]() OF=
OF=![]() ,
,
∴图中阴影部分面积=S扇形BOC-S△OCB=![]() -
-![]() ×3×
×3×![]() =
=![]() π-
π-![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案